27 Simple Linear Regression
Linear regression is a regression model which is a statistical technique for investigating and modeling the relationships between variables. If your data set only have one variable, or you just want to analyze one single variable in your data, you do not need regression at all. But you’d like to see how one variable affects another, how one changes with the another, or use one variable to predict another variable, regression may be your top choice. Linear regression assumes the relationships between variables or transformed variables is linear. Although the linear assumption is quite naive, it is a must starting point for understanding advanced regression models, and believe or not, the linear model is still popular at present because of its interpretability, and has a pretty decent performance for some problems.
27.1 Correlation
Relationship Between 2 Numerical Variables
We first define the linear correlation between two numerical variables. Depending on your research question, one may be classified as the explanatory variable and the other the response variable. However, in correlation, the two variables do not necessarily have such explanatory-response relationship, and they can be any numerical variables being interested. We will discuss the meaning of explanatory and response variable in the regression section.
Can you provide an example that two variables are associated? Here I provide some examples.
- height and weight
- income and age
- SAT/ACT math score and verbal score
- amount of time spent studying for an exam and exam grade
In each item, the two variables are related each other in some way. Usually the taller a person is, the heavier he is. Note that such relationship is not deterministic, but describe a general trend. We could have a 6’6” guy with 198 lbs, and a 5’9” with 220 lbs, but this an individual case, not an overall pattern. This concept is important because it is represented in the calculation of correlation coefficient and linear regression model.
Scatterplots
The most clear way to show the relationship between two numerical variables is to create a scatterplot. The overall pattern or relationship can be detected several ways in a scatterplot.
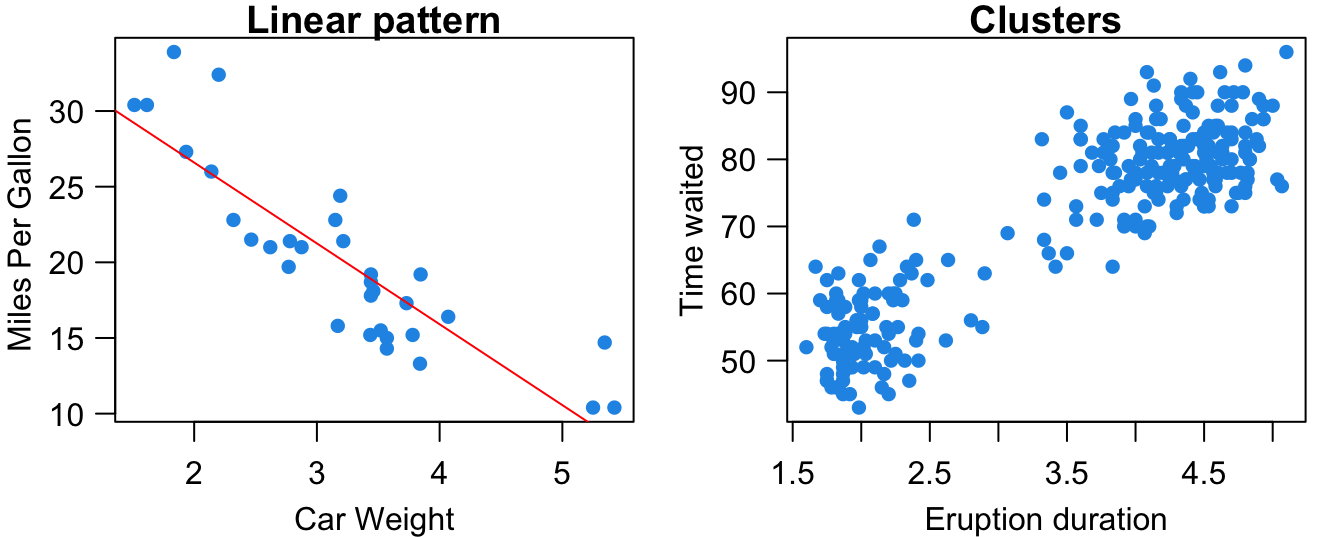
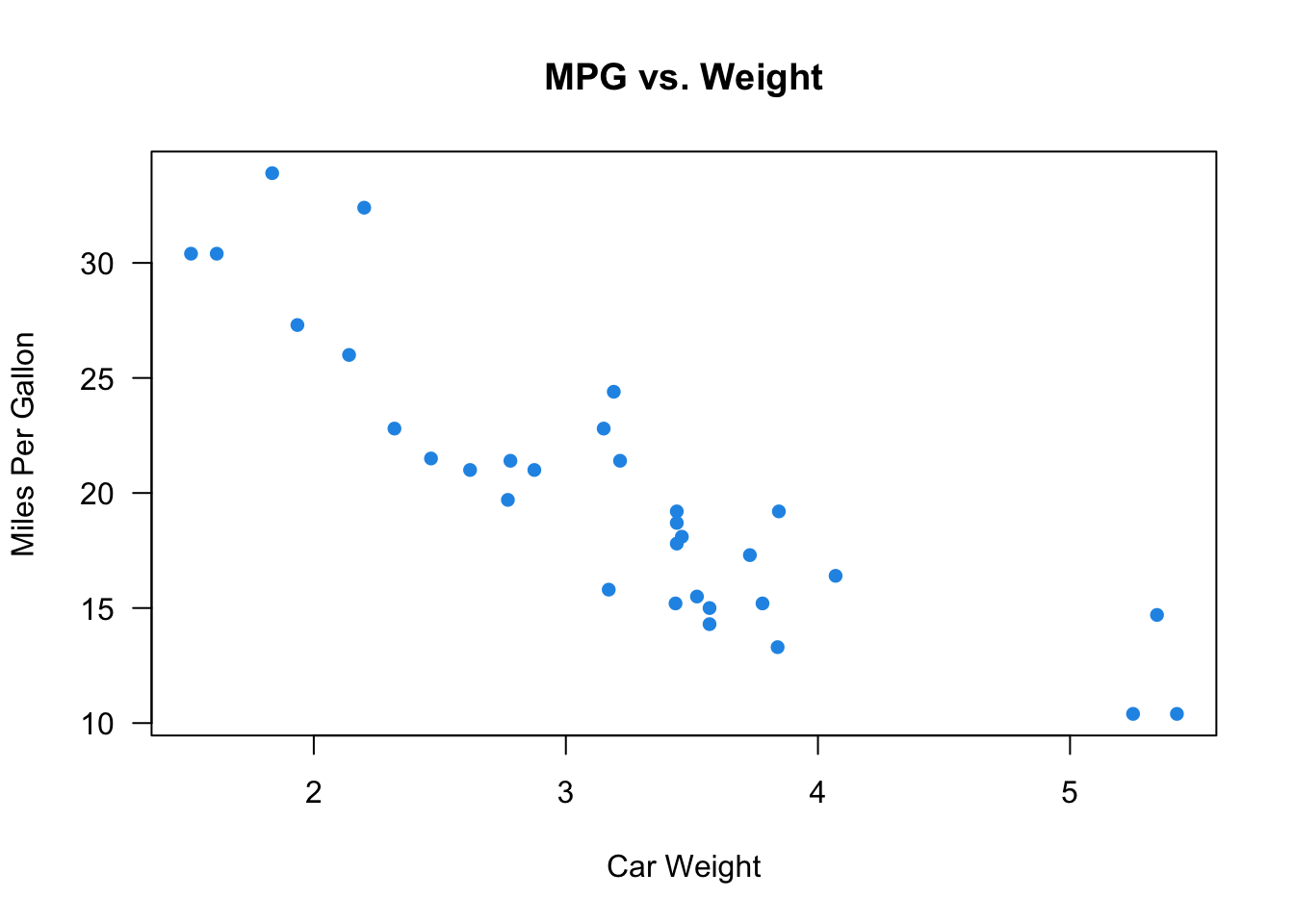
Form: As shown in Figure 27.1, the relationship between the two variables may be linear. Heavier cars tend to be less fuel efficient. The subjects in the data may be separated into two groups or clusters based on the value of the two variables. The volcano’s eruption duration and time waited are either small or large. Scatterplts can show other patterns such as quadratic, cubic or any other nonlinear relationships. In this chapter, we stay with the linear relationship.
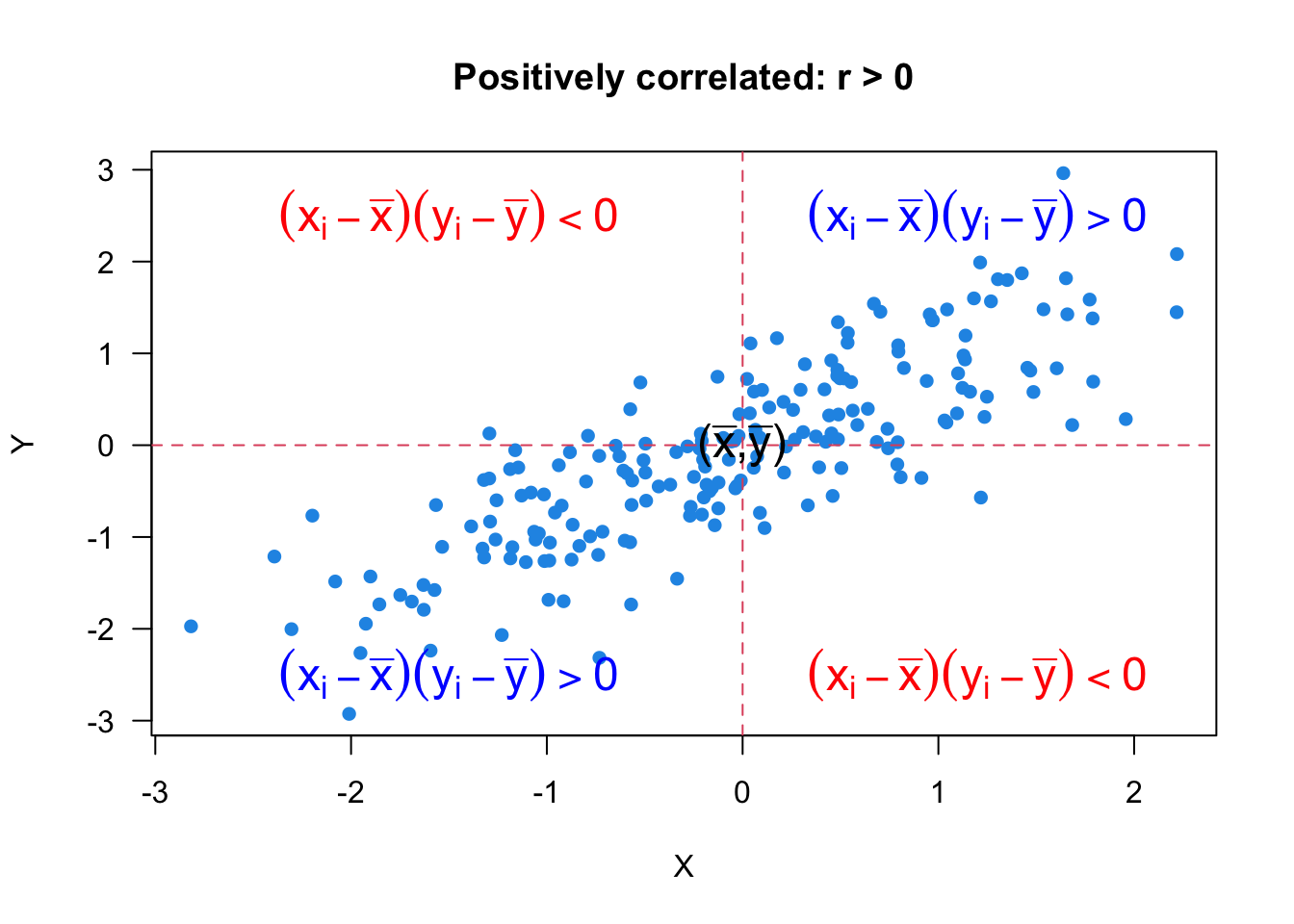
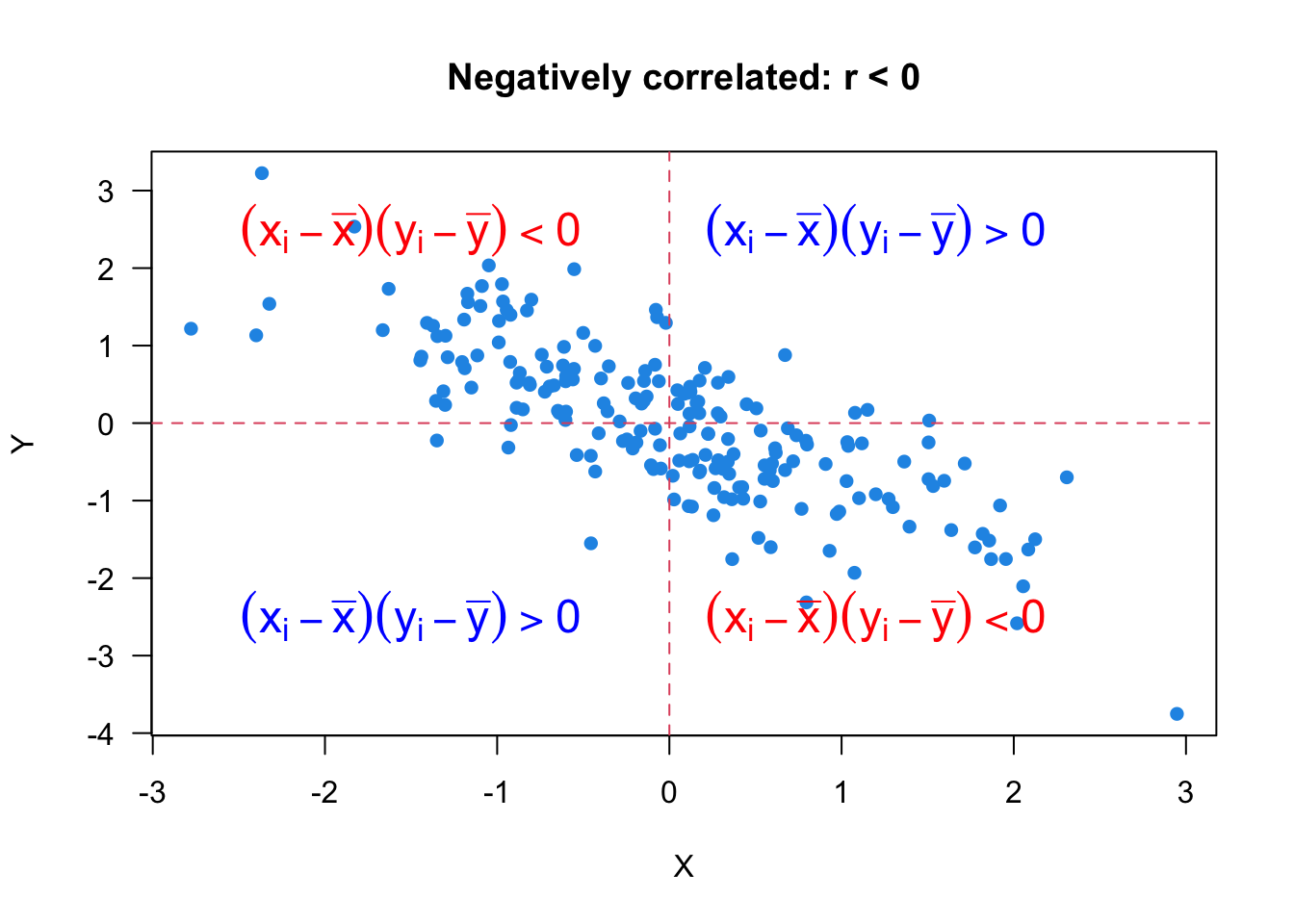
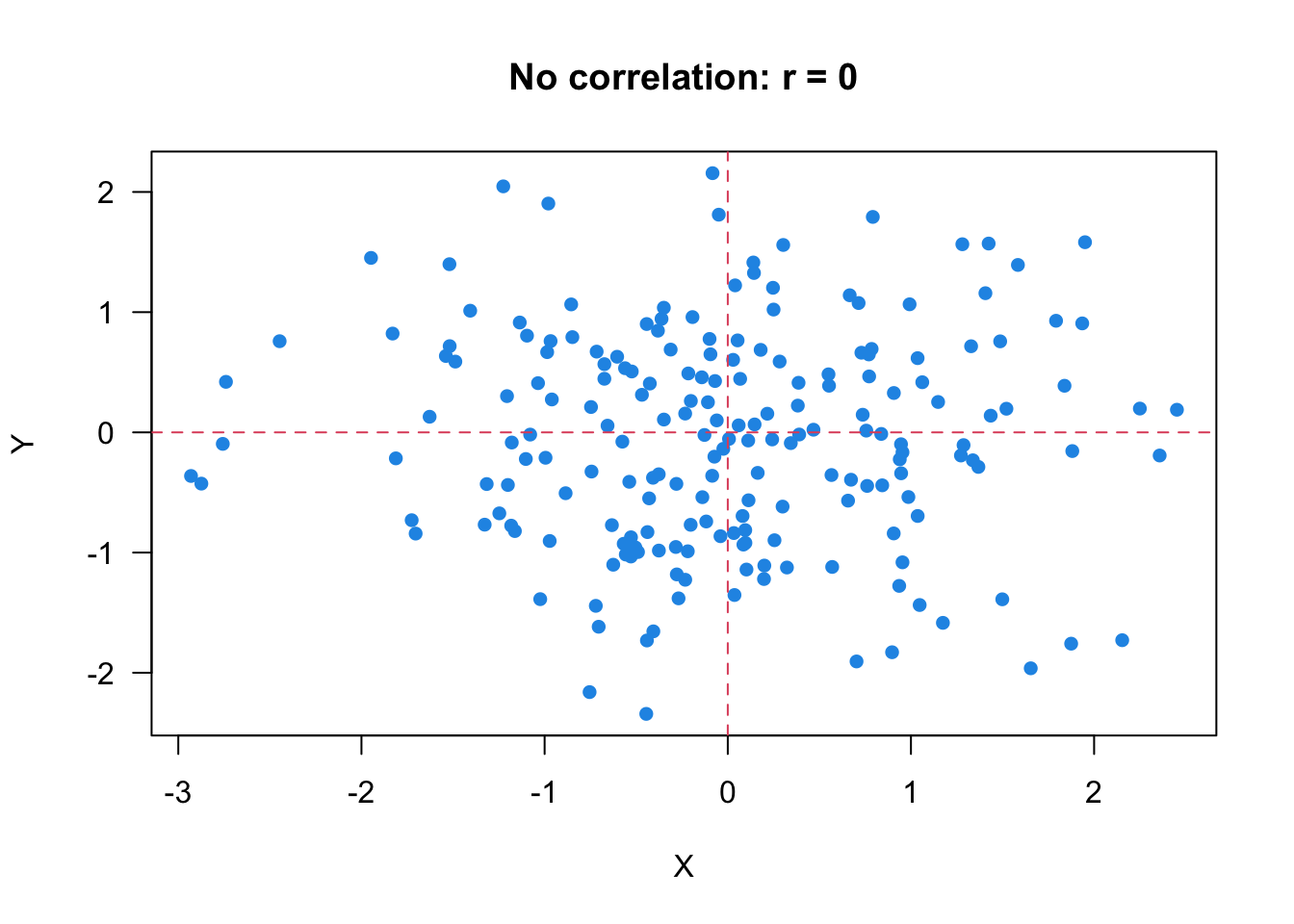
Direction: The variables can be positively associated or negatively associated, or not associated. In the scatterplot, the linear pattern is described by a line summarized by the data points in the plot. If the slope of the line is positive (negative), the two variables are positively (negatively) associated, meaning that one gets large as the other gets small. If the slope of the line is zero, the two variables have no association, and whether one variable’s value is large or small does not affect the other variable’s value.
Strength: Strength is how close the data points lie to the line or nonlinear curve trend in the scatter plot. The variables’ relationship is strong (weak) if the data points are pretty close (far away) to the line.
Although scatterplots can show form, direction, and strength of the relationship, we often want to have a numerical measure that can quantify these properties. If the relationship is linear, we use linear correlation coefficient to quantify the direction and strength of the linear relationship.
Linear Correlation Coefficient
The sample correlation coefficient, denoted by
This is the sample coefficient because the statistic is calculated by the sample data. 1
You don’t need to memorize the formula, but it would be great if you can understand how the formula is related to the scatter plot, and why the formula can quantify the direction and strength of the linear relationship.
First, the coefficient is between negative one and positive one,
Let’s look at Figure 27.2 and see how the formula and the scatter plot are related. Since
When
When
One property of
Last but not least. It is possible that there is a strong relationship between two variables, but they still have
The bottom row in Figure 27.5 shows several nonlinear
In R, we use the function cor() to calculate the correlation coefficient x and y. Here we use the built-in mtcars dataset, and calculate the correlation between the high miles per gallon (mpg) and car weight (wt). The coefficient is -0.87. Usually, when
In Python, we use the function corr() to calculate the correlation coefficient first_pd.Series.corr(second_pd.Series).
Here we use the built-in mtcars dataset, and calculate the correlation between the high miles per gallon (mpg) and car weight (wt). The coefficient is -0.87. Usually, when
import matplotlib.pyplot as plt
# Scatter plot of MPG vs. Weight
plt.scatter(mtcars['wt'], mtcars['mpg'],
color='blue')
plt.title('MPG vs. Weight')
plt.xlabel('Car Weight')
plt.ylabel('Miles Per Gallon')
plt.show()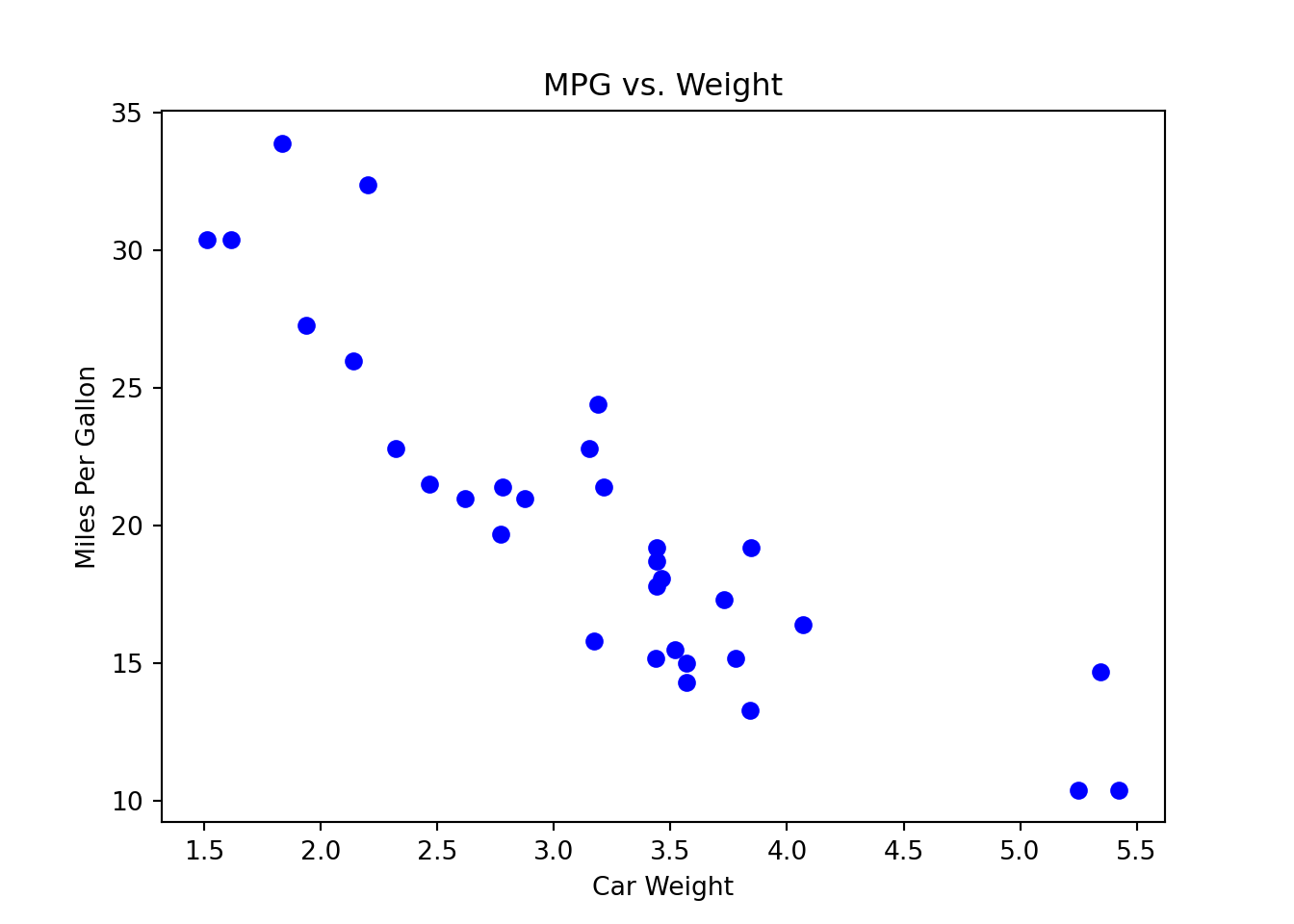
mtcars['wt'].corr(mtcars['mpg'])-0.8676593765172281
27.2 Meaning of Regression
What is Regression?
Regression models the relationship between one or more numerical/categorical response variables
Explanatory variables are also called independent variables, predictors, regressors, covariates, exogenous variables, and inputs. Response variables are also called dependent variables, targets, endogenous variables, outcome variables, outputs, and labels.
The followings are some examples.
Predict College GPA
Estimate how much Sales
How the Crime Rate
In regression, we use a regression function,
Let’s first pretend we know what the true regression function
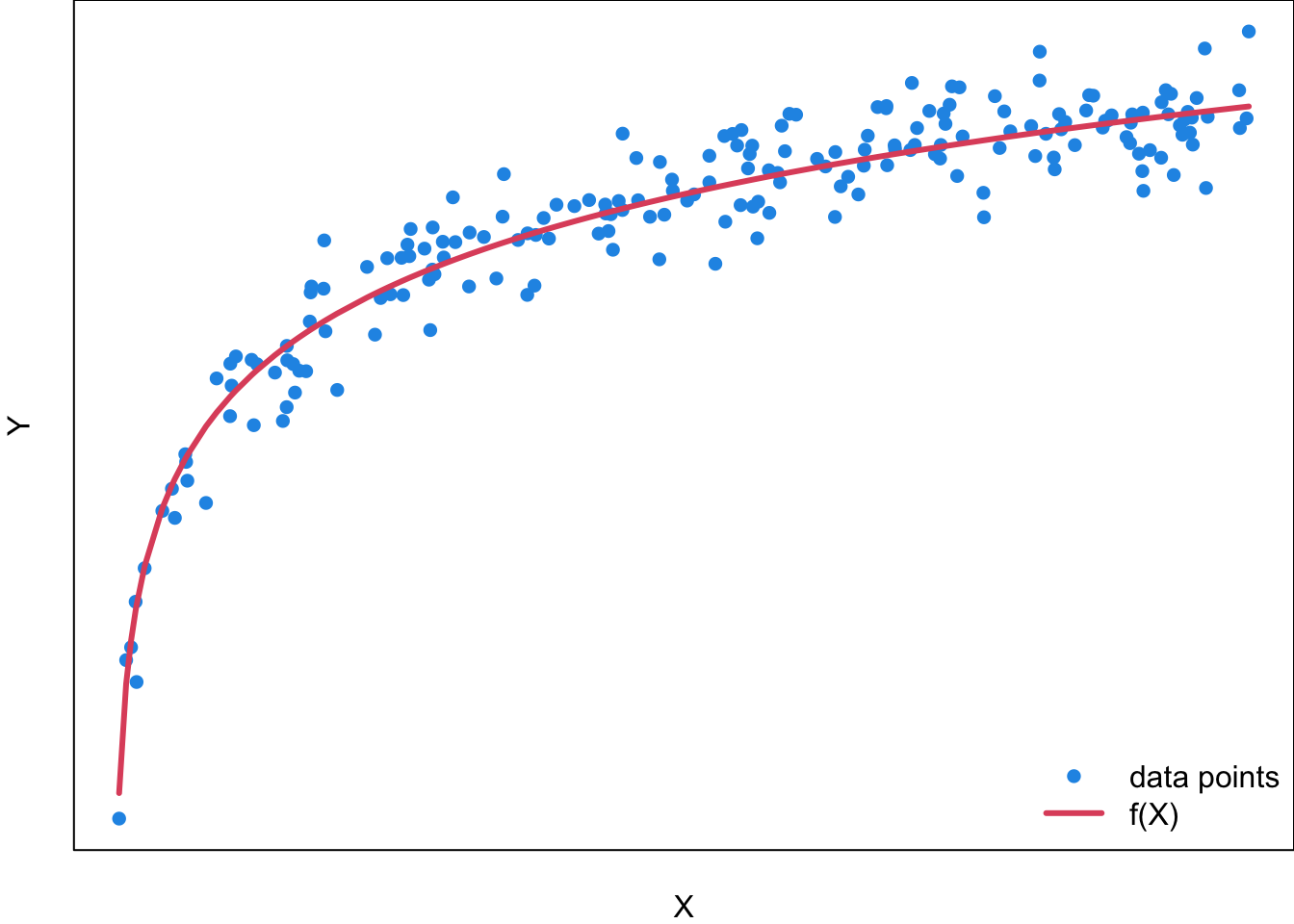
For a general regression model, the function needs not be linear, and could be of any type. Figure 27.6 is an example of a regression function
For example, if you want to use a student’s SAT/ACT Score (
Although
Now we have learned an important concept in regression: the regression function
Unknown Regression Function
Unfortunately the true underlying relationship between
Simple Linear Regression
A regression model can be very general, considering lots of variables simultaneously and modeling a complex nonlinear regression function. We learn how to walk before how to run. So let’s start with the very basic simple linear regression. The model is called “simple” because there is only one predictor
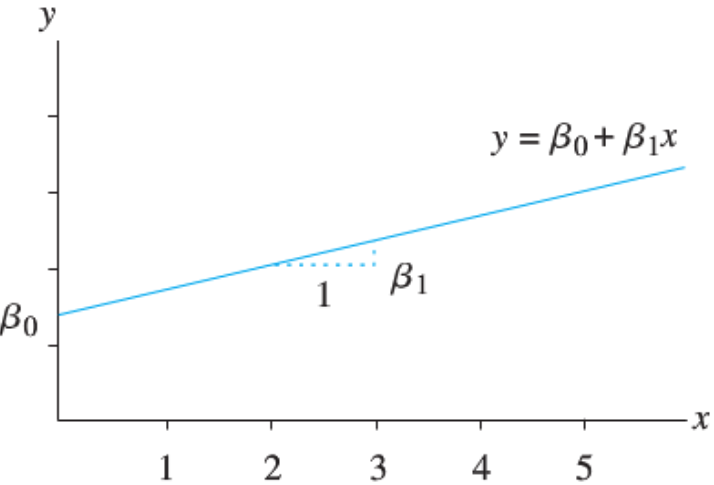
Let’s have a short math review. A linear function
The linearity assumption requires that
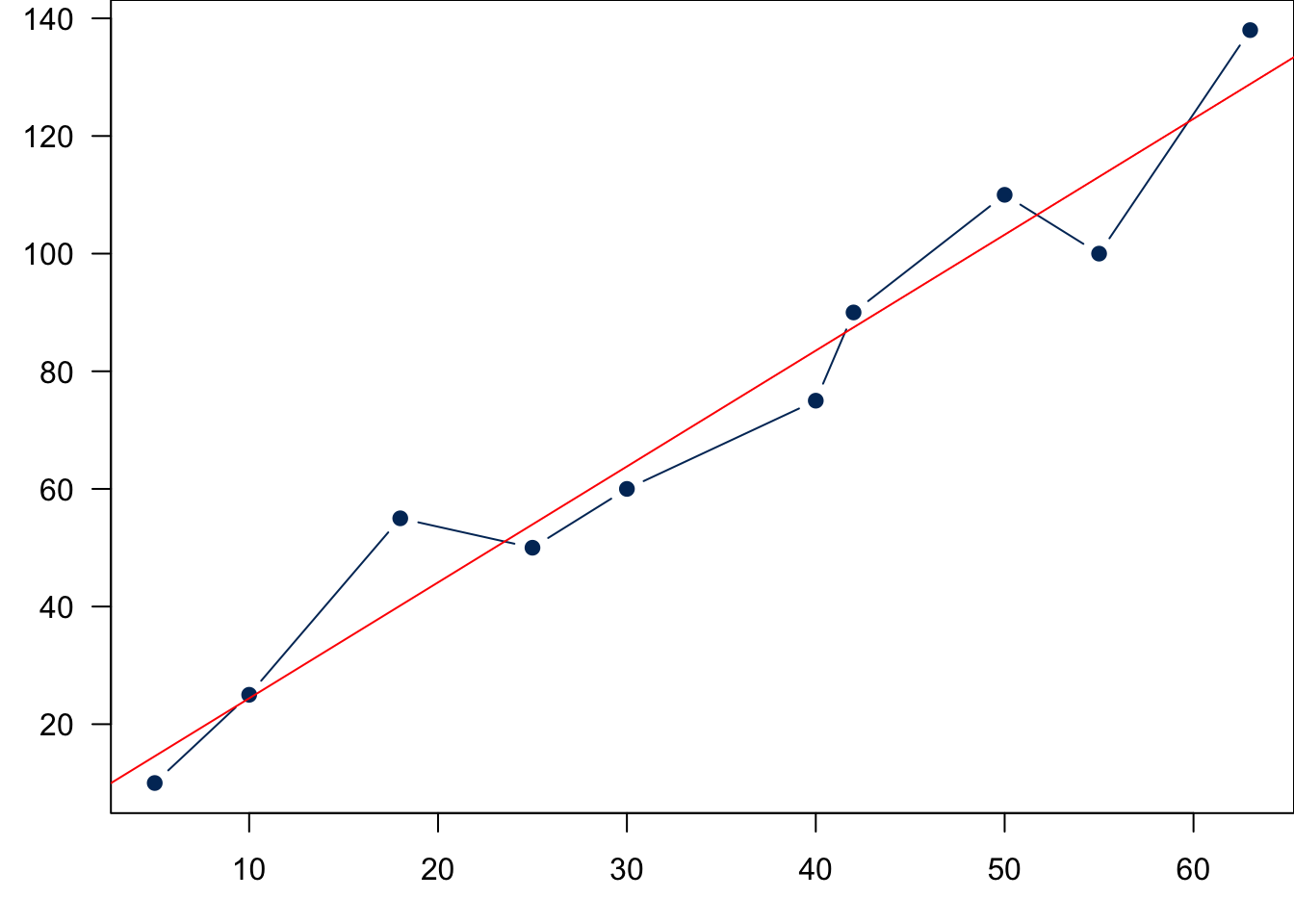
Sample Data: Relationship Between X and Y
Back to statistics. Remember that we want to use our sample data to estimate the unknown regression function or regression line. Suppose our data set is the
Now we need an additional variable to explain the deviations from the line and complete the modeling of data generating process. The deviation can be explained by a new variable
We learned that
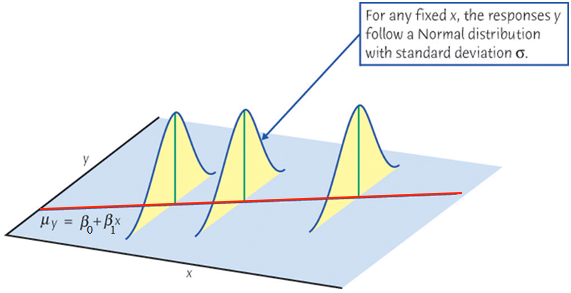
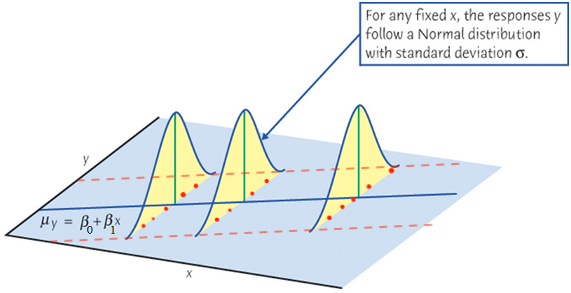
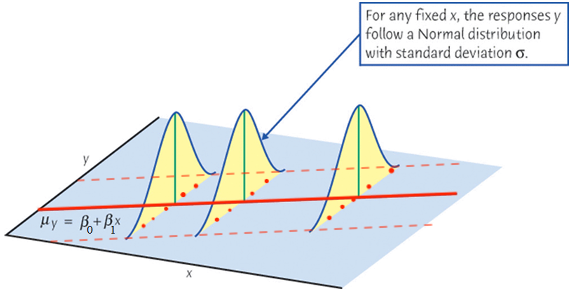
As we learned in random variable and sampling distribution, before we collect the sample,
When we collect our data, at any given level of
If at every level of
Finally let’s relate the figure to the equation
We never know the true regression function. In linear regression, we assume the function is linear. This assumption may be inappropriate or completely wrong. We need model adequacy checking to examine whether linearity assumption makes sense. At this moment, let’s put this issue aside, and assume the true function is linear.
Simple Linear Regression Model (Population)
We now formally write down the simple linear regression model.
For the
-
-
-
-
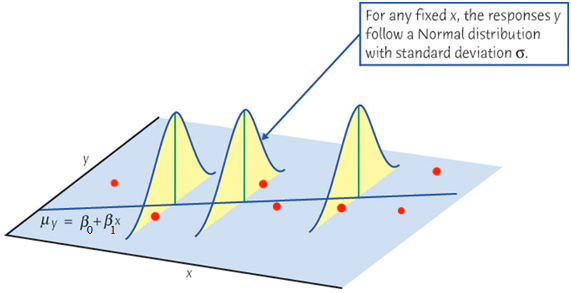
Important Features of Model
The setting
First, the mean of
-
- For variable or constant
Since
The mean response,
Second, for any
For a constant
Note that the variance of
Finally, if
For any fixed value of
Again,
Next section, we are going to learn how to estimate
27.3 Fitting a Regression Line
Idea of Fitting
Given the sample data
- Which sample regression line is the best?
- What are the best estimators,
The sample regression line is is
We are interested in
Ordinary Least Squares (OLS)
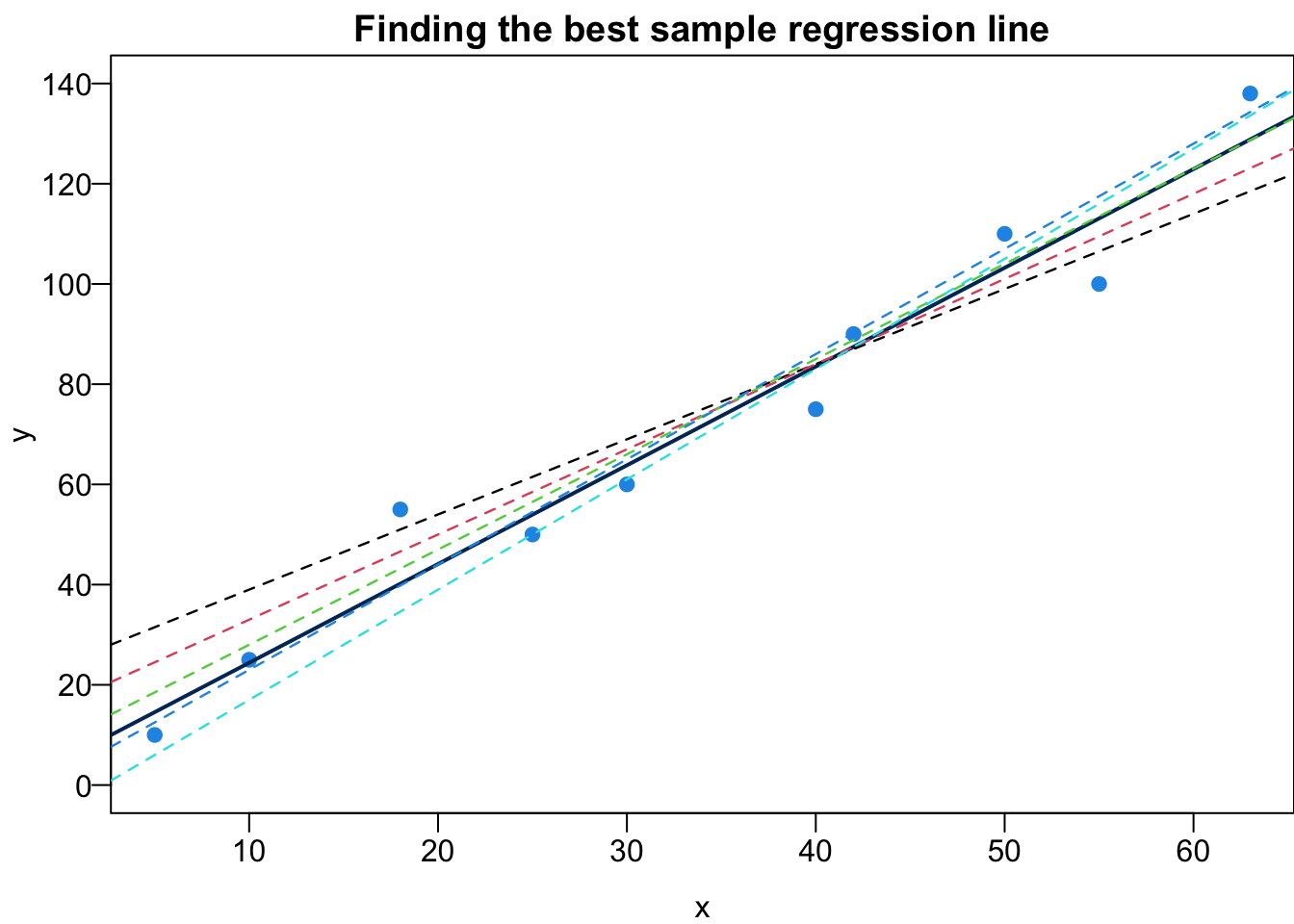
Given a data set, we could have many possible sample regression lines. In fact, there are infinitely many lines out there. Which one is the best?
To answer such question, we need to first define what “the best” mean. Here we want to choose
The residual,
The best sample regression line minimizes the sum of squared residuals
If
Before we actually find
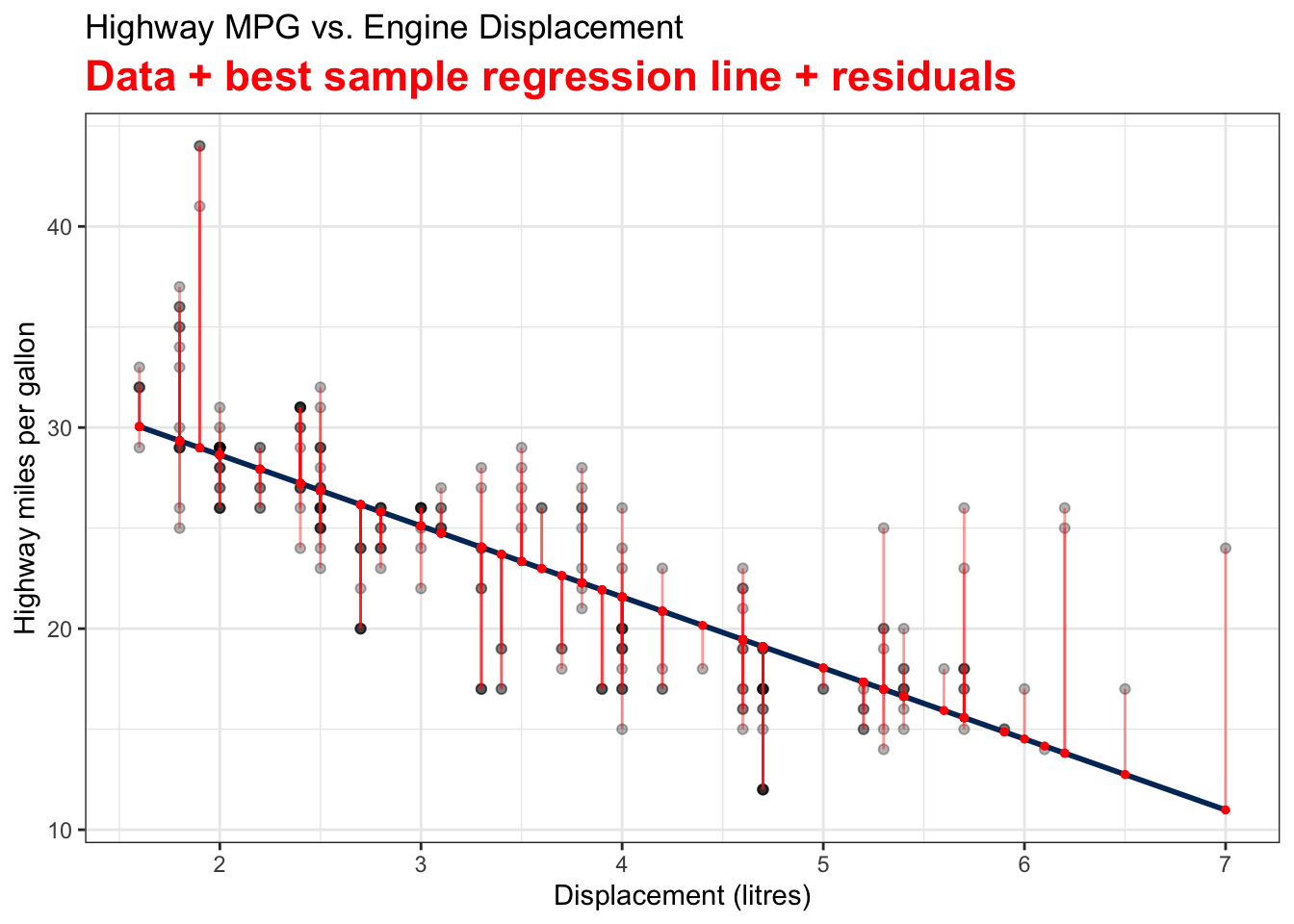
Visualizing Fitted Values and Residuals
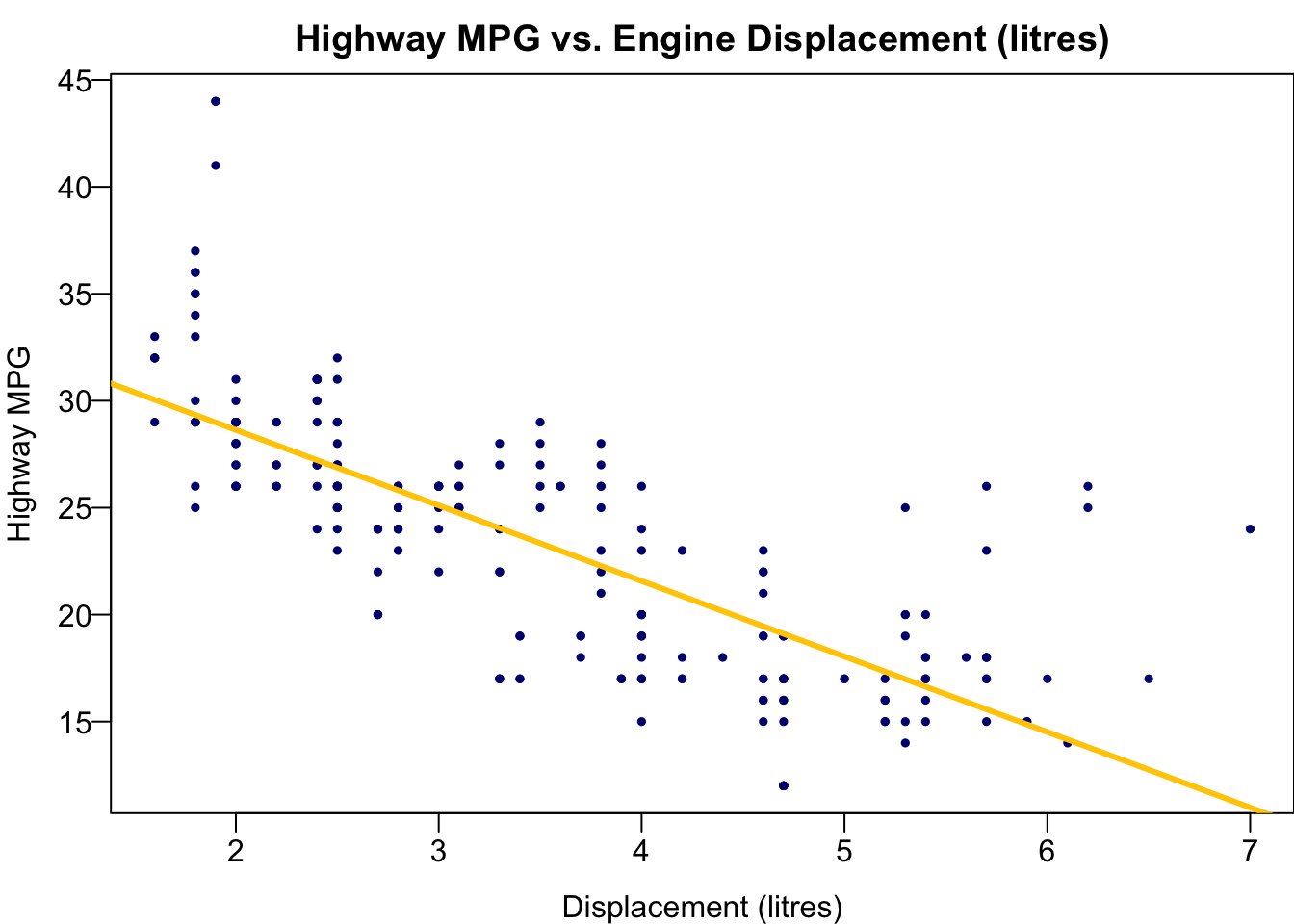
The two variables are the Car Displacement in litres and Highway Miles per Gallon. The scatter plot shows a negatively correlated relationship.
The best sample regression line
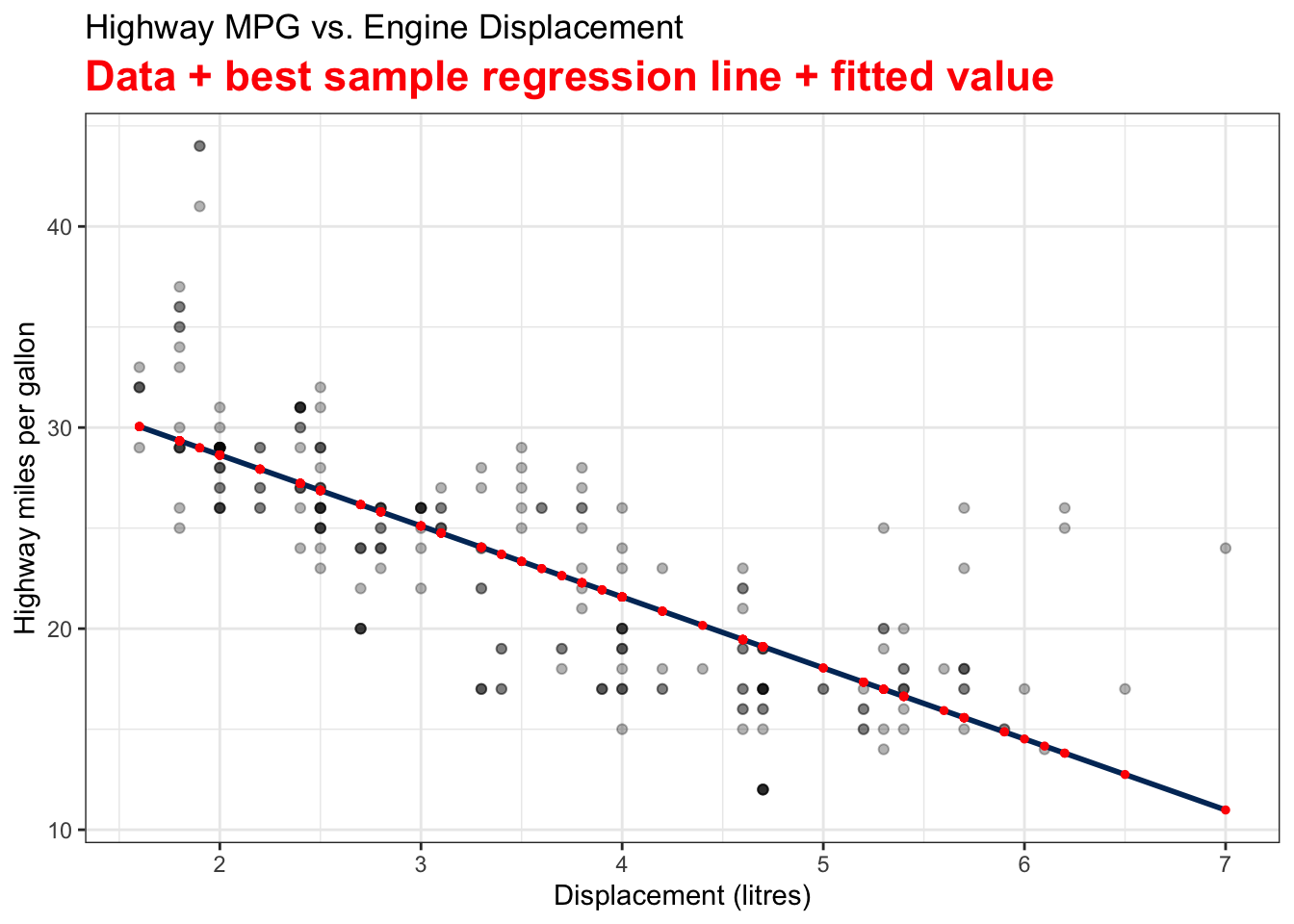
The residual
Least Squares Estimates (LSE)
It’s time to find the best
Mathematically,
It is an optimization problem. I leave it to you as an exercise. The formula of LSE is
Let’s see if we can get some intuition from the formula. First, the least squares regression line passes through the centroid
Nowadays we use computing software to get the estimates, but it’s good to to know the idea of OLS, and the properties of
We use the mpg data set in the ggplot2 package to demonstrate doing regression analysis in R. In particular, we grab the variable hwy as our response and disp as our predictor.
# A tibble: 234 × 11
manufacturer model displ year cyl trans drv cty hwy fl class
<chr> <chr> <dbl> <int> <int> <chr> <chr> <int> <int> <chr> <chr>
1 audi a4 1.8 1999 4 auto… f 18 29 p comp…
2 audi a4 1.8 1999 4 manu… f 21 29 p comp…
3 audi a4 2 2008 4 manu… f 20 31 p comp…
4 audi a4 2 2008 4 auto… f 21 30 p comp…
5 audi a4 2.8 1999 6 auto… f 16 26 p comp…
6 audi a4 2.8 1999 6 manu… f 18 26 p comp…
7 audi a4 3.1 2008 6 auto… f 18 27 p comp…
8 audi a4 quattro 1.8 1999 4 manu… 4 18 26 p comp…
9 audi a4 quattro 1.8 1999 4 auto… 4 16 25 p comp…
10 audi a4 quattro 2 2008 4 manu… 4 20 28 p comp…
# ℹ 224 more rows Highway MPG hwy vs. Displacement displ
First we create the scatter plot.
plot(x = mpg$displ, y = mpg$hwy,
las = 1, pch = 19, col = "navy", cex = 0.5,
xlab = "Displacement (litres)", ylab = "Highway MPG",
main = "Highway MPG vs. Engine Displacement (litres)")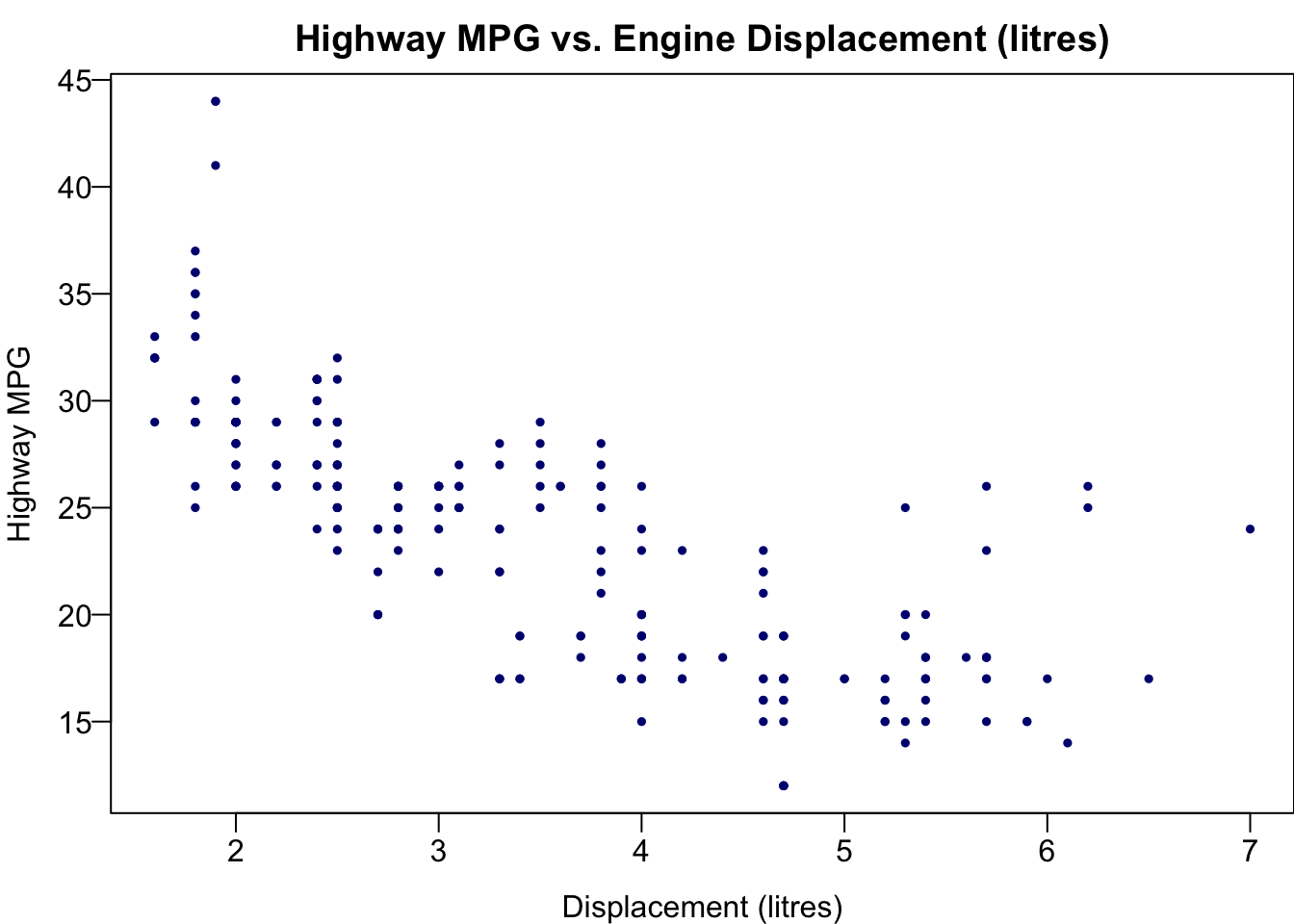
Fit Simple Linear Regression
To fit a linear regression, we use the lm() function because linear regression is a linear model. As we learned in ANOVA Chapter 24, we write the formula hwy ~ displ, and specify the data set mpg. We save the fitted result in the object reg_fit which is a R list. The output prints
For one unit (litre) increase of the displacement, we expect the highway MPG to be decreased, on average, by 3.53 miles.
reg_fit <- lm(formula = hwy ~ displ, data = mpg)
reg_fit
Call:
lm(formula = hwy ~ displ, data = mpg)
Coefficients:
(Intercept) displ
35.698 -3.531 typeof(reg_fit)[1] "list"## all elements in reg_fit
names(reg_fit) [1] "coefficients" "residuals" "effects" "rank"
[5] "fitted.values" "assign" "qr" "df.residual"
[9] "xlevels" "call" "terms" "model" ## use $ to extract an element of a list
reg_fit$coefficients(Intercept) displ
35.697651 -3.530589 Fitted Values of
## the first 5 observed response value y
mpg$hwy[1:5][1] 29 29 31 30 26## the first 5 fitted value y_hat
head(reg_fit$fitted.values, 5) 1 2 3 4 5
29.34259 29.34259 28.63647 28.63647 25.81200 ## the first 5 predictor value x
mpg$displ[1:5][1] 1.8 1.8 2.0 2.0 2.8length(reg_fit$fitted.values)[1] 234Add a Regression Line
To add the fitted regression line, we just put the fitted result reg_fit into the function abline().
We use the mpg data set in the ggplot2 package to demonstrate doing regression analysis in Python. In particular, we grab the variable hwy as our response and disp as our predictor.
manufacturer model displ year cyl trans drv cty hwy fl class
0 audi a4 1.8 1999 4 auto(l5) f 18 29 p compact
1 audi a4 1.8 1999 4 manual(m5) f 21 29 p compact
2 audi a4 2.0 2008 4 manual(m6) f 20 31 p compact
3 audi a4 2.0 2008 4 auto(av) f 21 30 p compact
4 audi a4 2.8 1999 6 auto(l5) f 16 26 p compact Highway MPG hwy vs. Displacement displ
First we create the scatter plot.
plt.scatter(mpg['displ'], mpg['hwy'],
color='blue')
plt.title('Highway MPG vs. Engine Displacement (litres)')
plt.xlabel('Displacement (litres)')
plt.ylabel('Highway MPG')
plt.show()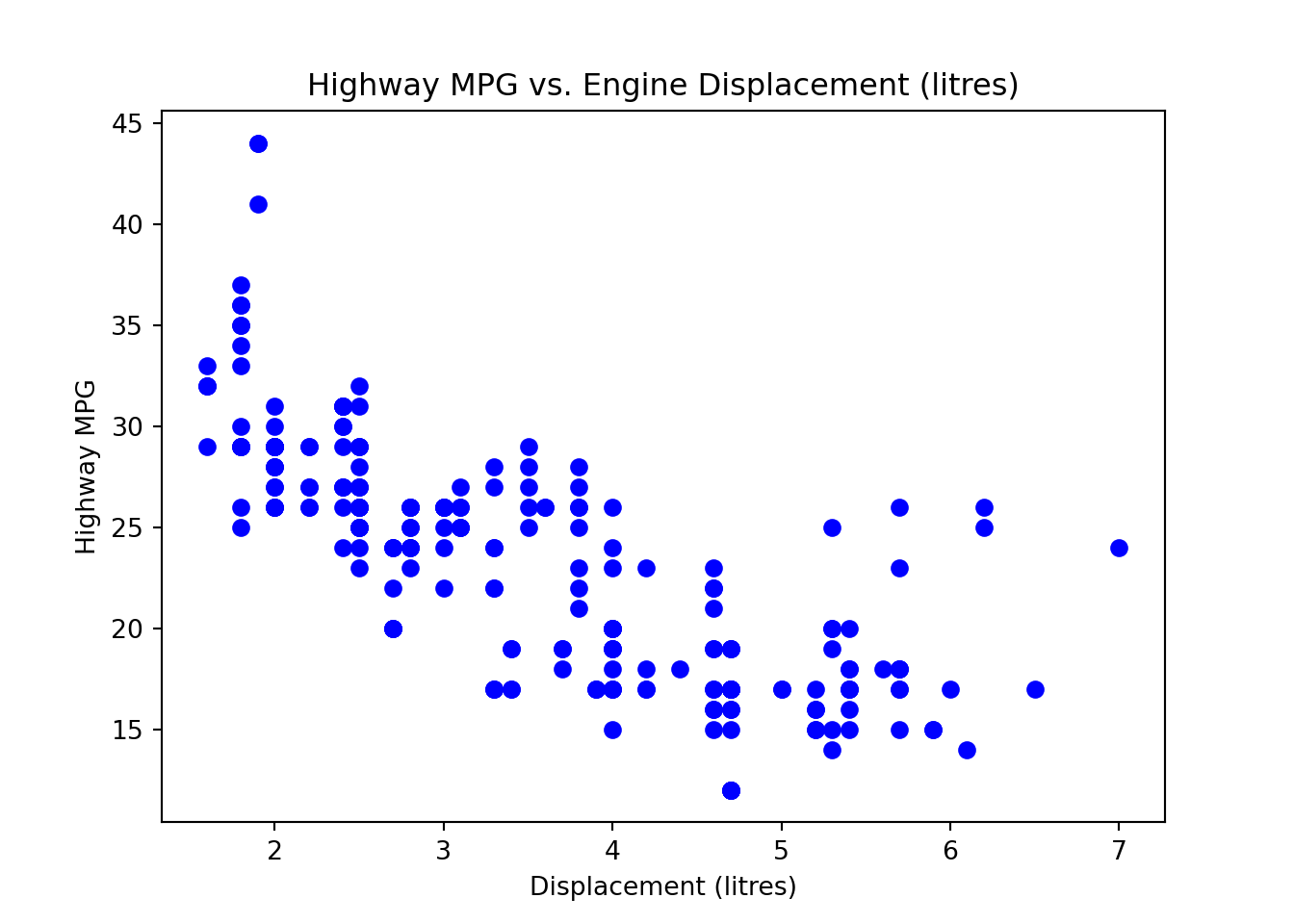
Fit Simple Linear Regression
To fit a linear regression, we use the ols() function. As we learned in ANOVA Chapter 24, we write the formula 'hwy ~ displ', and specify the data set mpg. We save the fitted result in the object reg_fit.
reg_fit.summary() will output the OLS regression results. The output prints
For one unit (litre) increase of the displacement, we expect the highway MPG to be decreased, on average, by 3.53 miles.
from statsmodels.formula.api import ols
# Fit a simple linear regression model
reg_fit = ols('hwy ~ displ', data=mpg).fit()
reg_fit.summary()| Dep. Variable: | hwy | R-squared: | 0.587 |
| Model: | OLS | Adj. R-squared: | 0.585 |
| Method: | Least Squares | F-statistic: | 329.5 |
| Date: | Thu, 12 Jun 2025 | Prob (F-statistic): | 2.04e-46 |
| Time: | 11:50:08 | Log-Likelihood: | -645.62 |
| No. Observations: | 234 | AIC: | 1295. |
| Df Residuals: | 232 | BIC: | 1302. |
| Df Model: | 1 | ||
| Covariance Type: | nonrobust |
| coef | std err | t | P>|t| | [0.025 | 0.975] | |
| Intercept | 35.6977 | 0.720 | 49.555 | 0.000 | 34.278 | 37.117 |
| displ | -3.5306 | 0.195 | -18.151 | 0.000 | -3.914 | -3.147 |
| Omnibus: | 45.280 | Durbin-Watson: | 0.954 |
| Prob(Omnibus): | 0.000 | Jarque-Bera (JB): | 90.192 |
| Skew: | 0.961 | Prob(JB): | 2.60e-20 |
| Kurtosis: | 5.357 | Cond. No. | 11.3 |
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
## All fields and methods in the reg_fit object
dir(reg_fit)['HC0_se', 'HC1_se', 'HC2_se', 'HC3_se', '_HCCM', '__class__', '__delattr__', '__dict__', '__dir__', '__doc__', '__eq__', '__format__', '__ge__', '__getattribute__', '__getstate__', '__gt__', '__hash__', '__init__', '__init_subclass__', '__le__', '__lt__', '__module__', '__ne__', '__new__', '__reduce__', '__reduce_ex__', '__repr__', '__setattr__', '__sizeof__', '__str__', '__subclasshook__', '__weakref__', '_abat_diagonal', '_cache', '_data_attr', '_data_in_cache', '_get_robustcov_results', '_get_wald_nonlinear', '_is_nested', '_transform_predict_exog', '_use_t', '_wexog_singular_values', 'aic', 'bic', 'bse', 'centered_tss', 'compare_f_test', 'compare_lm_test', 'compare_lr_test', 'condition_number', 'conf_int', 'conf_int_el', 'cov_HC0', 'cov_HC1', 'cov_HC2', 'cov_HC3', 'cov_kwds', 'cov_params', 'cov_type', 'df_model', 'df_resid', 'diagn', 'eigenvals', 'el_test', 'ess', 'f_pvalue', 'f_test', 'fittedvalues', 'fvalue', 'get_influence', 'get_prediction', 'get_robustcov_results', 'info_criteria', 'initialize', 'k_constant', 'llf', 'load', 'model', 'mse_model', 'mse_resid', 'mse_total', 'nobs', 'normalized_cov_params', 'outlier_test', 'params', 'predict', 'pvalues', 'remove_data', 'resid', 'resid_pearson', 'rsquared', 'rsquared_adj', 'save', 'scale', 'ssr', 'summary', 'summary2', 't_test', 't_test_pairwise', 'tvalues', 'uncentered_tss', 'use_t', 'wald_test', 'wald_test_terms', 'wresid']## parameter coefficient estimates
reg_fit.paramsIntercept 35.697651
displ -3.530589
dtype: float64 Fitted Values of
## the first 5 observed response value y
mpg['hwy'].head(5).valuesarray([29, 29, 31, 30, 26])## the first 5 fitted value y_hat
reg_fit.fittedvalues.head(5).valuesarray([29.3425912 , 29.3425912 , 28.63647344, 28.63647344, 25.81200239])## the first 5 predictor value x
mpg['displ'].head(5).valuesarray([1.8, 1.8, 2. , 2. , 2.8])len(reg_fit.fittedvalues)234Add a Regression Line
To add the fitted regression line, we add another plot with y values being reg_fit.fittedvalues. ::: {.cell layout-align=“center”}
plt.scatter(x=mpg['displ'], y=mpg['hwy'], color='navy')
plt.plot(mpg['displ'], reg_fit.fittedvalues, color='#FFCC00', linewidth=3)
plt.title('Highway MPG vs. Engine Displacement (litres)')
plt.xlabel('Displacement (litres)')
plt.ylabel('Highway MPG')
plt.show()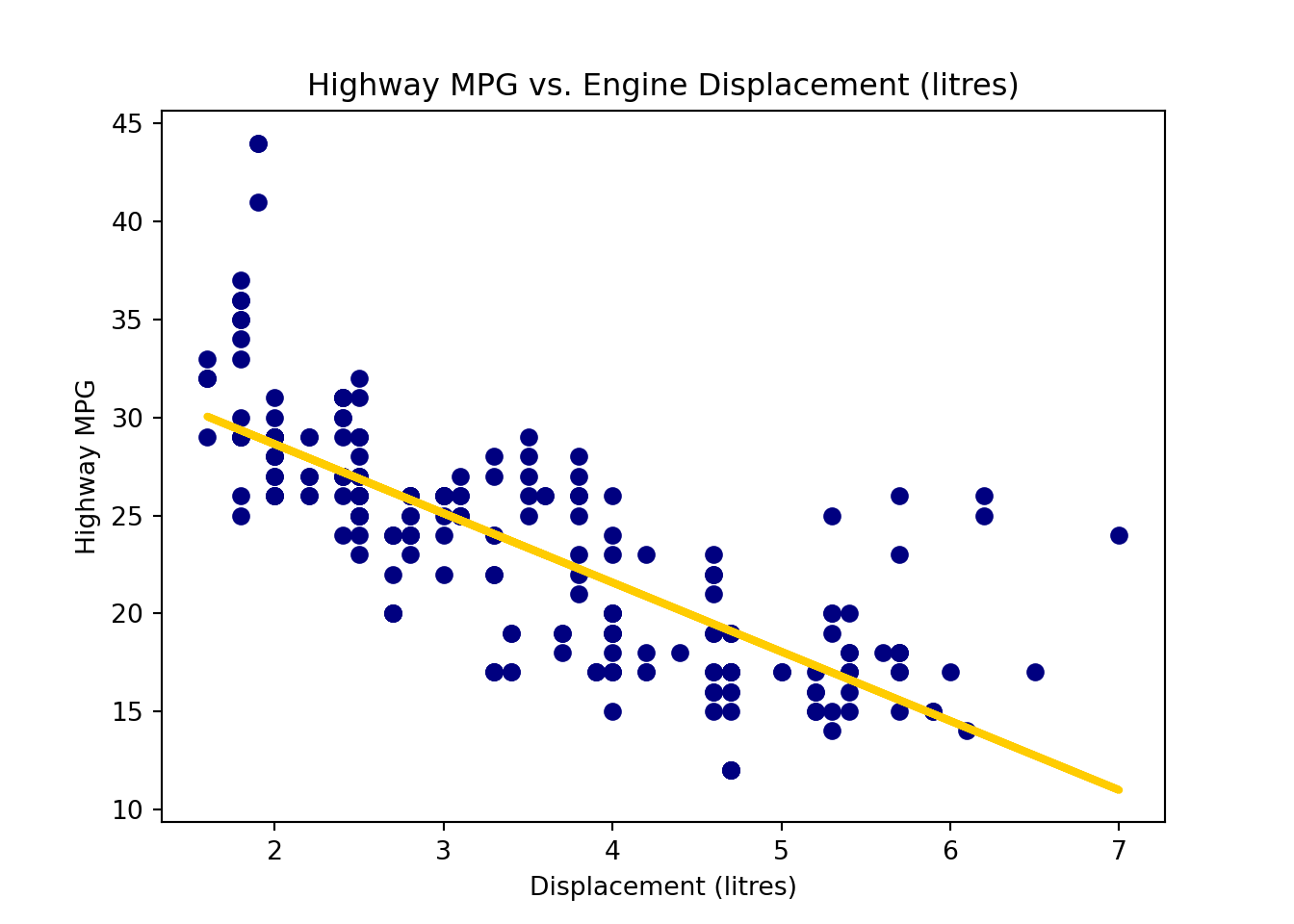
:::
Estimation for
We can think of
The variance of residuals is
The degrees of freedom is the number of values in the final calculation of a statistic that are free to vary. It is equal to the sample size minus the number of parameters estimated. In simple linear regression, we estimate
Remember that a sum of squares has a corresponding degrees of freedom.
By the way,
Please be careful that R provide the standard error
The standard error Residual standard error. The degrees of freedom is
(summ_reg_fit <- summary(reg_fit))...
Residual standard error: 3.836 on 232 degrees of freedom
...We can grab the summ_reg_fit by summ_reg_fit$sigma.
# lots of fitted information saved in summary(reg_fit)!
names(summ_reg_fit) [1] "call" "terms" "residuals" "coefficients"
[5] "aliased" "sigma" "df" "r.squared"
[9] "adj.r.squared" "fstatistic" "cov.unscaled" # residual standard error (sigma_hat)
summ_reg_fit$sigma[1] 3.835985It is not hard to compute the
# from reg_fit
sum(reg_fit$residuals^2) / reg_fit$df.residual[1] 14.71478The standard error reg_fit.mse_resid, short for mean square error of residuals.
If we want the standard error,
import numpy as np
reg_fit.mse_resid14.71478021118735np.sqrt(reg_fit.mse_resid)3.835984907580757# from reg_fit to compute MS_res
np.sum(reg_fit.resid ** 2) / reg_fit.df_resid14.714780211187357
27.4 Confidence Intervals and Hypothesis Testing for
We’ve obtained the point estimators of
Confidence Intervals for
Note that
Therefore, the
The
To grab the confidence interval for confint() function. By default, the confidence level is 95%, but any other level can be specified. We say we are 95% confident that one unit increase of displacement will result in a decrease in highway miles per gallon on average by 3.91 to 3.15 miles.
confint(reg_fit, level = 0.95) 2.5 % 97.5 %
(Intercept) 34.278353 37.11695
displ -3.913828 -3.14735To grab the confidence interval for conf_int() of the fitted object. By default, the confidence level is 95%, but any other level can be specified. We say we are 95% confident that one unit increase of displacement will result in a decrease in highway miles per gallon on average by 3.91 to 3.15 miles.
reg_fit.conf_int(alpha=0.05) 0 1
Intercept 34.278353 37.11695
displ -3.913828 -3.14735Estimated regression line
histogram of estimates from the simulated dataset
🟠 population β0
🔵 estimated b0 for the current data.
histogram of estimates from the simulated dataset
🟠 population β1
🔵 estimated b1 for the current data.
import {lm as lm} from "@chrispahm/linear-models-in-observable-notebooks"
import {summary as summary} from "@chrispahm/linear-models-in-observable-notebooks"
import {Histogram as Histogram} from "@d3/histogram"
import {Scrubber as Scrubber} from "@mbostock/scrubber"
Hypothesis Testing
The hypothesis testing for
-
- Test statistic: Under
- Reject
-
- Test statistic: Under
- Reject
The two-sided test result for summ_reg_fit$coefficients. The first row is for intercept and the second for the slope. The columns from left to right are LSEs, the standard errors of LSEs, the
summ_reg_fit...
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 35.6977 0.7204 49.55 <2e-16 ***
displ -3.5306 0.1945 -18.15 <2e-16 ***
...summ_reg_fit$coefficients Estimate Std. Error t value Pr(>|t|)
(Intercept) 35.697651 0.7203676 49.55477 2.123519e-125
displ -3.530589 0.1945137 -18.15085 2.038974e-46Notice that the testing output is for the two-sided test with hypothesized value being equal to zero. The first row tests whether or not
he two-sided test result for
reg_fit.summary()| Dep. Variable: | hwy | R-squared: | 0.587 |
| Model: | OLS | Adj. R-squared: | 0.585 |
| Method: | Least Squares | F-statistic: | 329.5 |
| Date: | Thu, 12 Jun 2025 | Prob (F-statistic): | 2.04e-46 |
| Time: | 11:50:09 | Log-Likelihood: | -645.62 |
| No. Observations: | 234 | AIC: | 1295. |
| Df Residuals: | 232 | BIC: | 1302. |
| Df Model: | 1 | ||
| Covariance Type: | nonrobust |
| coef | std err | t | P>|t| | [0.025 | 0.975] | |
| Intercept | 35.6977 | 0.720 | 49.555 | 0.000 | 34.278 | 37.117 |
| displ | -3.5306 | 0.195 | -18.151 | 0.000 | -3.914 | -3.147 |
| Omnibus: | 45.280 | Durbin-Watson: | 0.954 |
| Prob(Omnibus): | 0.000 | Jarque-Bera (JB): | 90.192 |
| Skew: | 0.961 | Prob(JB): | 2.60e-20 |
| Kurtosis: | 5.357 | Cond. No. | 11.3 |
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
reg_fit.pvaluesIntercept 2.123519e-125
displ 2.038974e-46
dtype: float64Notice that the testing output and the p-values reg_fit.pvalues are for the two-sided test with hypothesized value being equal to zero. The first row tests whether or not
Interpretation of Testing Results
Suppose we do the test
Test of Significance of Regression
Rejecting
the straight-line model is adequate.
better results could be obtained with a more complicated model.
Rejecting
27.5 Analysis of Variance (ANOVA) Approach
The testing for
First let me ask you a question.
If we have sample data for
If there is another variable
Losing such information hurts. With no information about the relationship between
The deviation of
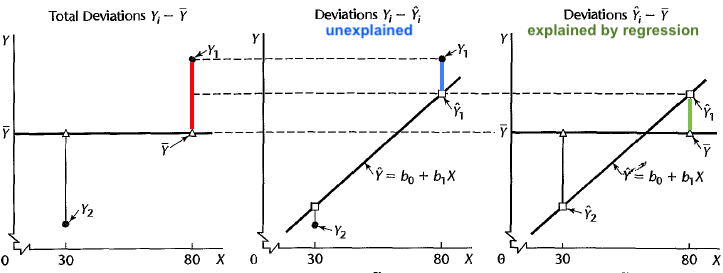
Partition of Deviation
The total deviation of
Total deviation = Deviation explained by regression + unexplained deviation
or
Figure 27.20 illustrates the deviation partition. Look at the point
Now if the positive correlation between
Finally, the remaining part of deviation that cannot be explained by
Sum of Squares (SS)
The deviation partition leads to the sum of squares identity
Total Sum of Squares
Their corresponding degrees of freedom is
or
The total sum of squares quantifies the sum of squared deviation from the mean, and
ANOVA for Testing Significance of Regression
The sum of squares and degrees of freedom identities allow us the make an ANOVA table as below. But what is this ANOVA table is for? It is used for testing overall significance of regression, that is, whether or not the regression model has explanatory power for explaining the variation of the response. When the regression model has explanatory power, all or some of its predictors are correlated with the response, and their corresponding regression coefficient is nonzero.
| Source of Variation | SS | df | MS | F |
|
|---|---|---|---|---|---|
| Regression | 1 | ||||
| Residual | |||||
| Total |
In other words, ANONA is for the test
A larger value of
-
Note that ANOVA is designed to test the
To get the ANOVA table, we put the fitted result into the function anova(). For simple linear regression, the ANOVA
anova(reg_fit)Analysis of Variance Table
Response: hwy
Df Sum Sq Mean Sq F value Pr(>F)
displ 1 4847.8 4847.8 329.45 < 2.2e-16 ***
Residuals 232 3413.8 14.7
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1summ_reg_fit$coefficients Estimate Std. Error t value Pr(>|t|)
(Intercept) 35.697651 0.7203676 49.55477 2.123519e-125
displ -3.530589 0.1945137 -18.15085 2.038974e-46summ_reg_fit$coefficients[2, 3] ^ 2[1] 329.4533To get the ANOVA table, we put the fitted result into the function sm.stats.anova_lm(). For simple linear regression, the ANOVA
import statsmodels.api as sm
sm.stats.anova_lm(reg_fit) df sum_sq mean_sq F PR(>F)
displ 1.0 4847.833384 4847.833384 329.453333 2.038974e-46
Residual 232.0 3413.829009 14.714780 NaN NaNreg_fit.tvaluesIntercept 49.554769
displ -18.150849
dtype: float64reg_fit.tvalues.iloc[1] ** 2329.45333294759047reg_fit.fvalue329.45333294759075Coefficient of Determination
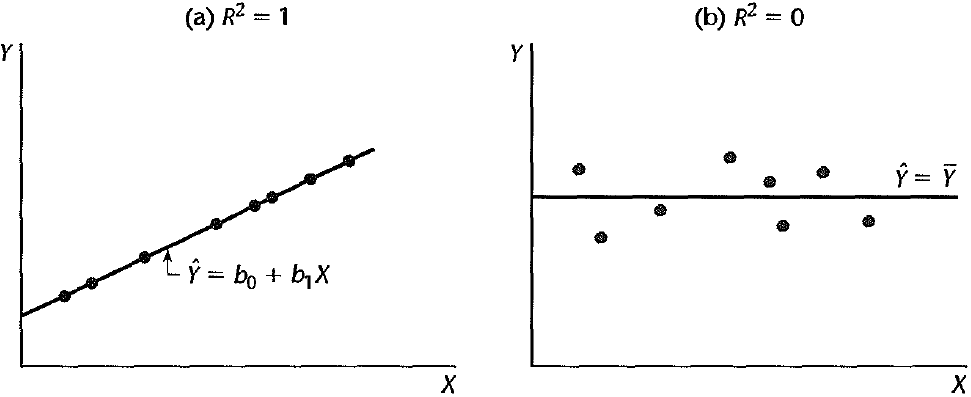
The coefficient of determination or
Figure 27.21 shows two extreme cases.
(a)
(b)
In (a), fitted values are equal to true observations. The regression model explains all the variation in
The summ_reg_fit$r.squared to get the value. The variable disp explains about 59% of the variation of hwy.
summ_reg_fit...
Residual standard error: 3.836 on 232 degrees of freedom
Multiple R-squared: 0.5868, Adjusted R-squared: 0.585
...summ_reg_fit$r.squared[1] 0.5867867The reg_fit.rsquared to get the value. The variable disp explains about 59% of the variation of hwy.
reg_fit.rsquared0.58678667239890427.6 Prediction
Prediction is one of our goals when we perform regression analysis. We want to use
When we talk about prediction, we refer to the predictor and response whose values haven’t seen in the data. For example, if our data have three
Predicting the Mean Response
With the predictor value
The mean
The
Well, no need to memorize the formula. But could you answer the following question?
We will have the shortest confidence interval for
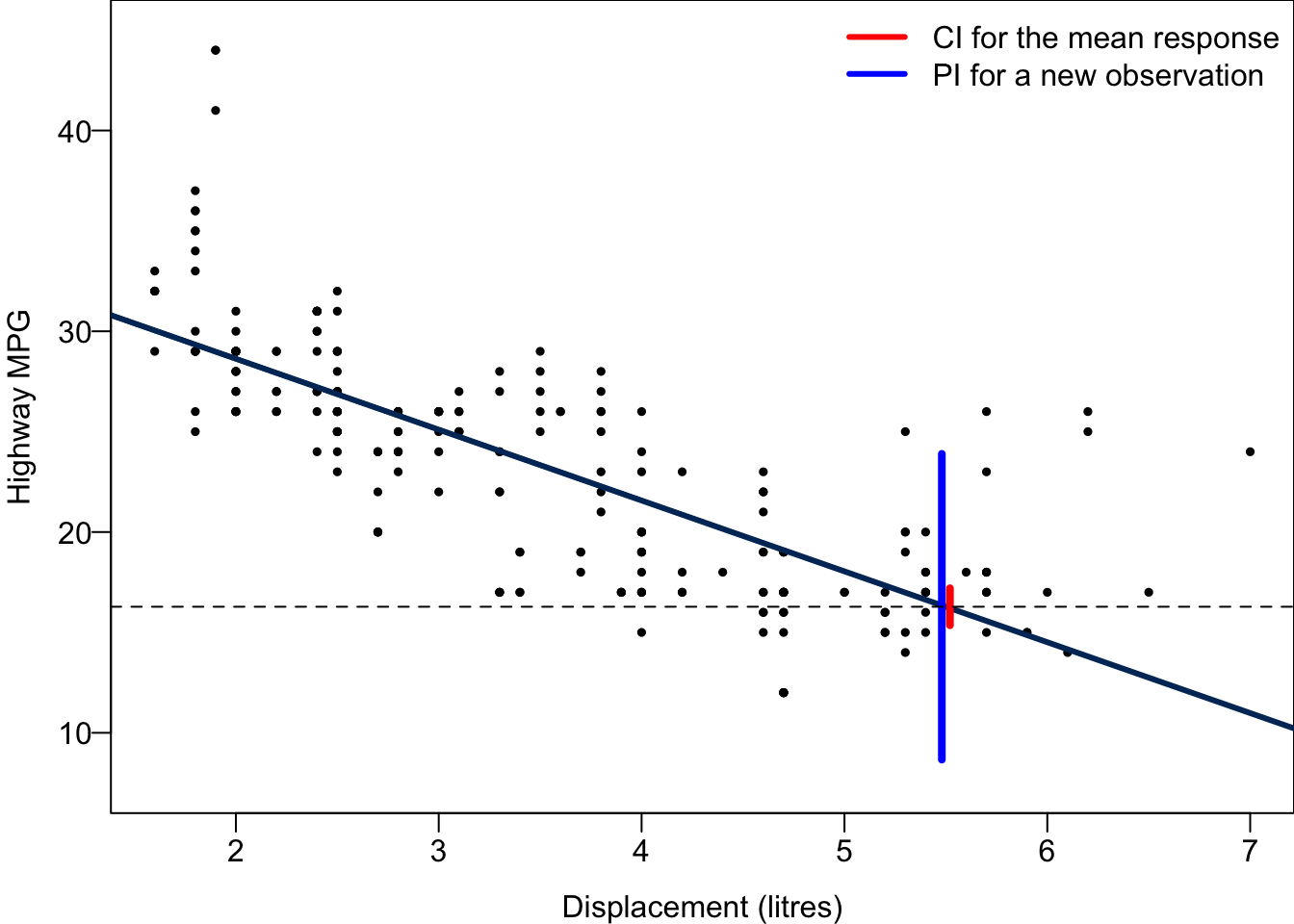
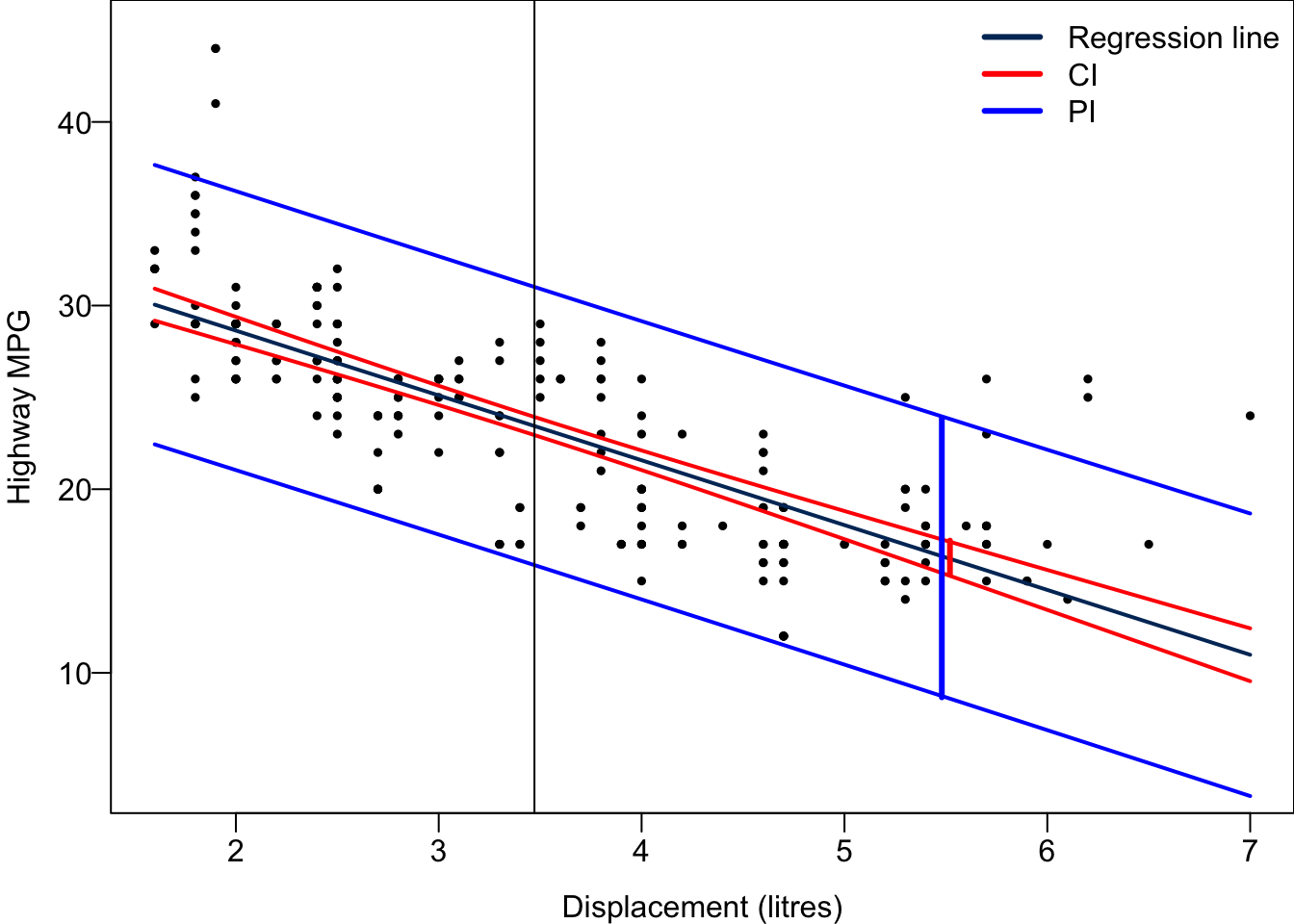
Predicting New Observations
We want to predict not only the mean level of response at some predictor value, but also the value of a new observation,
Do you see the difference? Previously we care about the mean response level, but here we predict an individual response value. There are thousand of millions of cars having displacement 5.5 liters. If we’d like to know the average miles per gallon or general fuel efficiency performance for the cars with displacement 5.5, we are predicting the mean response. When we want to predict the miles per gallon of a specific car whose displacement is 5.5, we predicting a new observation. The car is an individual outcome drawn from those thousand of millions of cars.
A point estimator for
The
A confidence interval is for a unknown parameter. We call the interval prediction interval because
The PI is wider as it includes the uncertainty about
To predict either the mean response or a new observation, we use the function predict(). The first argument is out fitted object reg_fit. Then we need to provide the predictor value for prediction in the argument newdata. Be careful that it has to be a data frame type, and variable’s name should be exactly the same as the predictor’s name in the original data set mpg when we fit the regression. If we want to get the confidence interval for the mean response, we specify “confidence” in the argument interval. If instead we want the prediction interval for a new response, we specify “predict”.
## CI for the mean response
predict(reg_fit, newdata = data.frame(displ = 5.5), interval = "confidence", level = 0.95) fit lwr upr
1 16.27941 15.35839 17.20043## PI for the new observation
predict(reg_fit, newdata = data.frame(displ = 5.5), interval = "predict", level = 0.95) fit lwr upr
1 16.27941 8.665682 23.89314To predict either the mean response or a new observation, we use the method get_prediction(). The first argument exog is the values for which you want to predict. exog means exogenous variables. Be careful that it has to be array_like type.
If we want to get the confidence interval for the mean response, predict.conf_int() provides that. If instead we want the prediction interval for a new response, we need to check the predict.summary_frame(). The prediction interval is saved in ‘obs_ci_lower’ and ‘obs_ci_upper’.
new_data = pd.DataFrame({'displ': [5.5]})
predict = reg_fit.get_prediction(new_data)
predict.conf_int()array([[15.35839096, 17.20043427]])summary_frame = predict.summary_frame(alpha=0.05)
summary_frame[['mean_ci_lower', 'mean_ci_upper']] mean_ci_lower mean_ci_upper
0 15.358391 17.200434summary_frame[['obs_ci_lower', 'obs_ci_upper']] obs_ci_lower obs_ci_upper
0 8.665682 23.893144The 95% CI for the mean hwy when disp = 5.5 is between 15.36 and 17.2, while The 95% PI for hwy of a car with disp = 5.5 is between 8.67 and 23.89. The PI is much wider than the CI because the variance of
Code
par(mar = c(3, 3, 0, 0), mgp = c(2, 0.5, 0), mfrow = c(1, 1))
## Data and regression line
plot(x = mpg$displ, y = mpg$hwy, las = 1, pch = 19, cex = 0.5,
ylim = c(7.5, 45), xlab = "Displacement (litres)",
ylab = "Highway MPG")
legend("topright", c("CI for the mean response", "PI for a new observation"),
col = c("red", "blue"), lwd = c(3, 3), bty = "n")
abline(reg_fit, col = "#003366", lwd = 3)
segments(x0 = 5.52, y0 = 15.35839, y1 = 17.20043, col = "red", lwd = 4)
segments(x0 = 5.48, y0 = 8.665682, y1 = 23.89314, col = "blue", lwd = 4)
abline(h = 16.27941, lty = 2)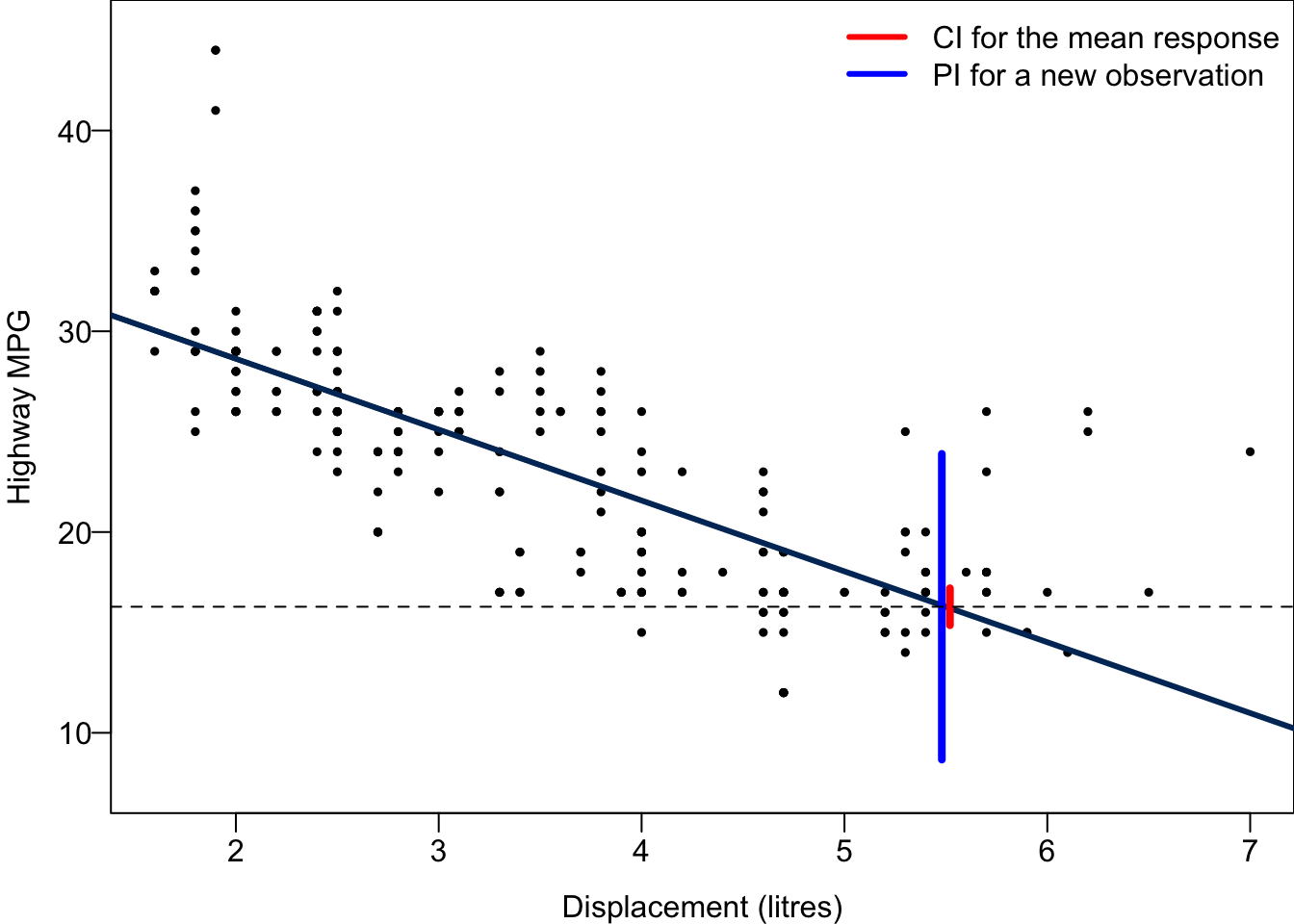
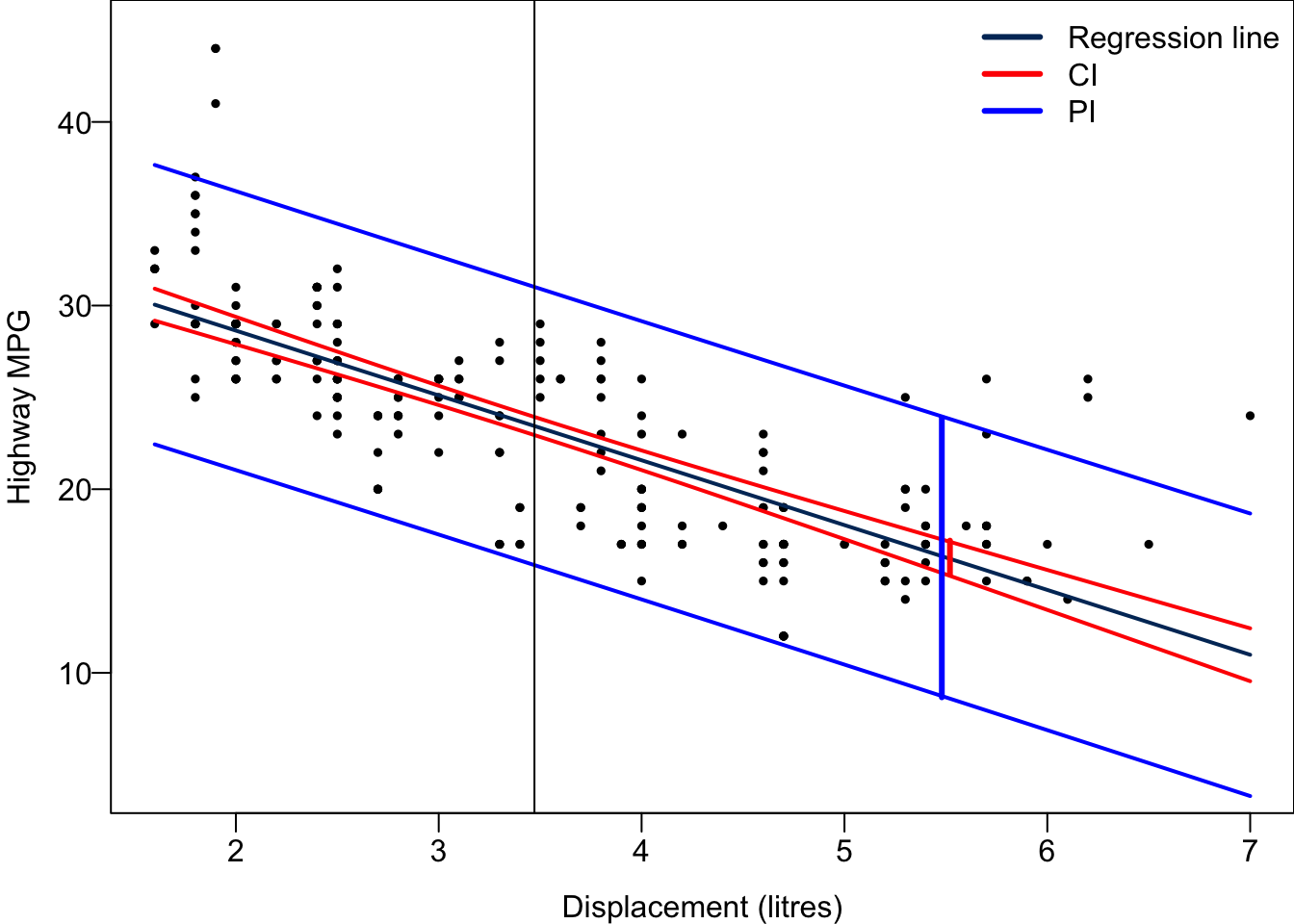
For every possible value of
27.7 Simulation-based Inference
We can use bootstrap to estimate the regression coefficients with uncertainty quantification without assuming or relying on normal distribution. Instead of doing distribution-based inference, we are doing simulation-based inference. Please go to Chapter 15 to review the idea of bootstrapping.
In simple linear regression, we perform bootstrap inference step by step as follows.
Bootstrap new samples
For each bootstrapped sample, we fit a simple linear regression model to it, and estimate the corresponding slope. If we have
Use the distribution of the bootstrapped slopes to construct a confidence interval. We plot the histogram of those
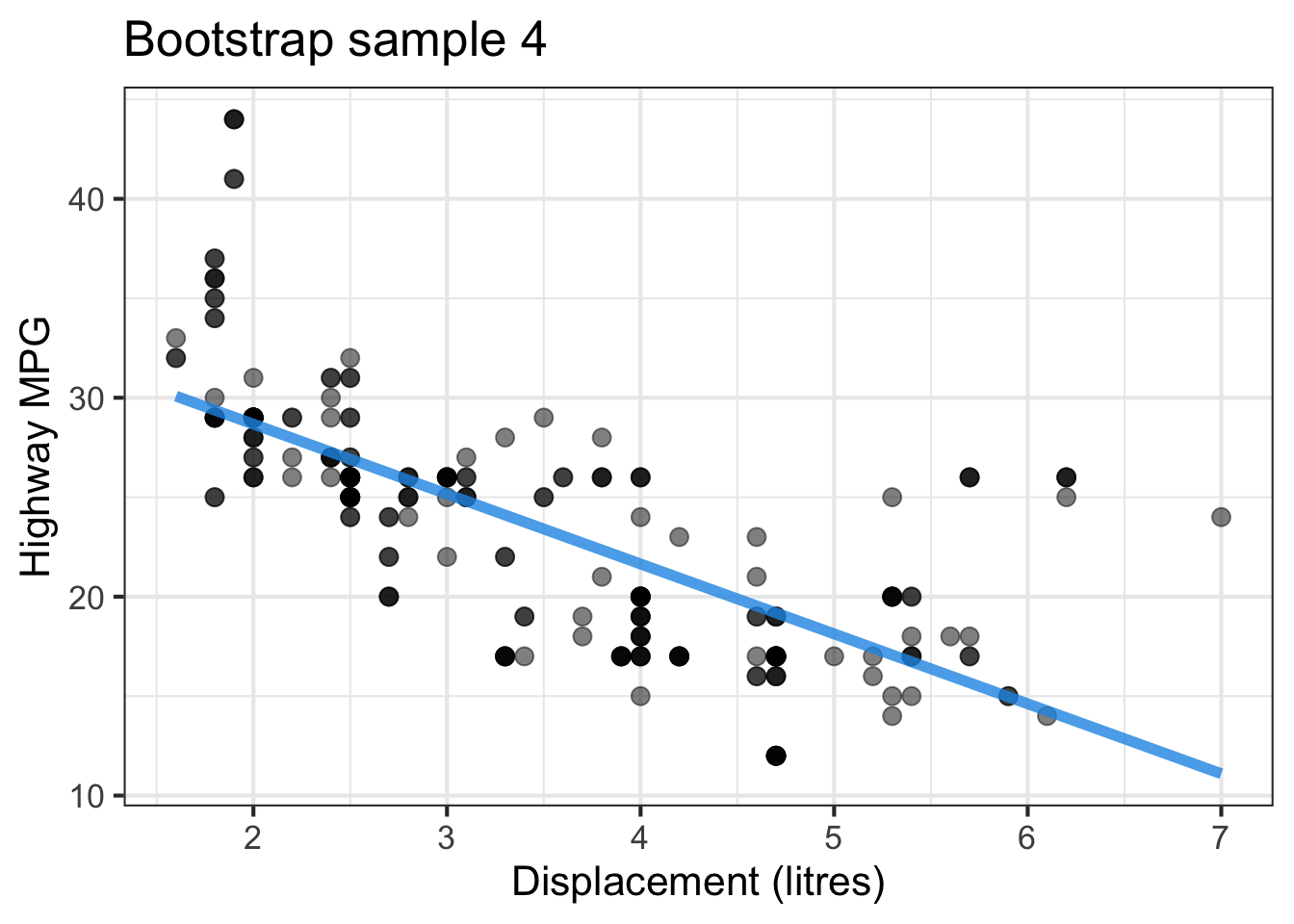
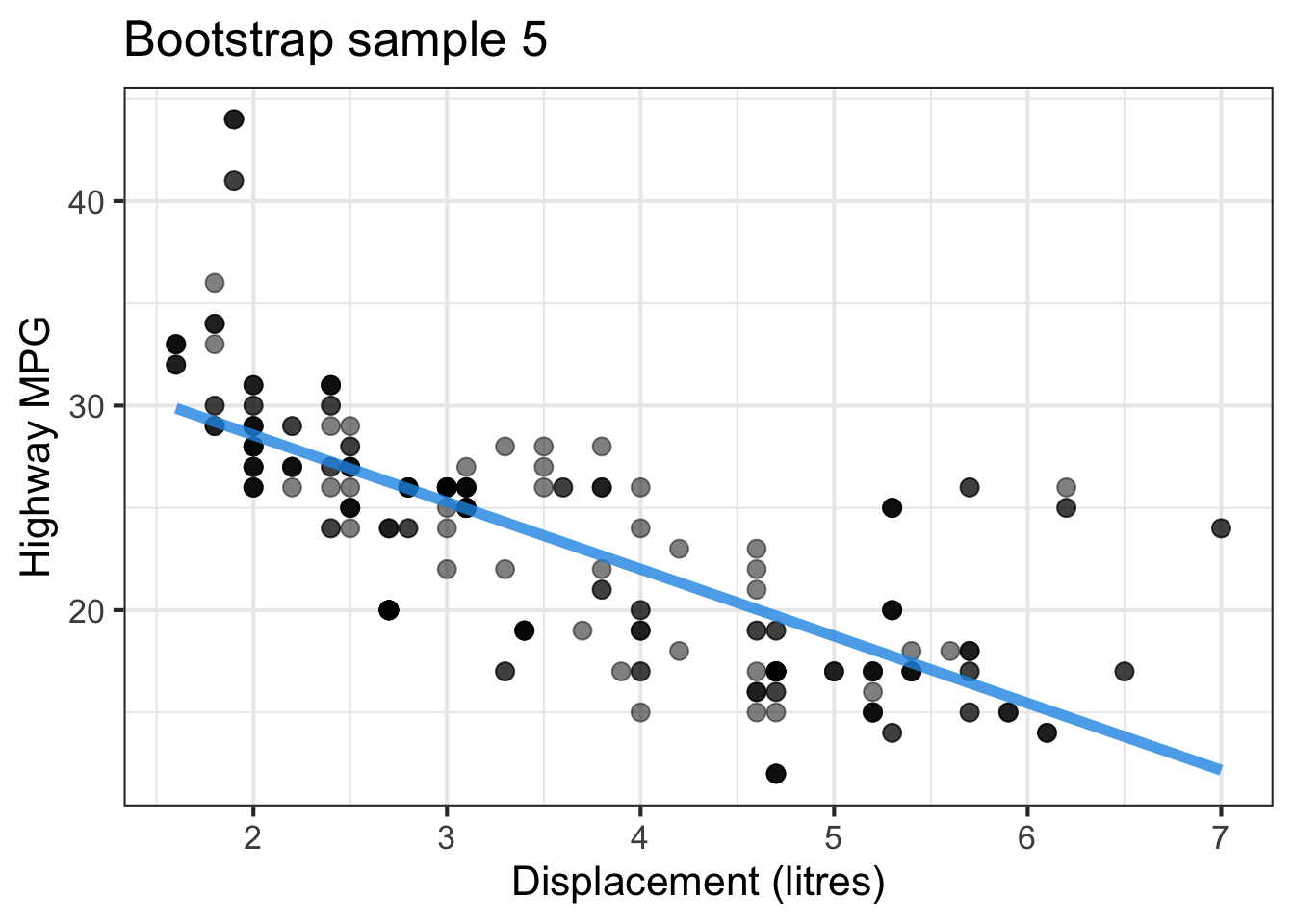
The followings show the scatter plot of hwy vs. displ from the original mpg data set and 5 bootstrapped samples with their linear regression fitted line. First, you can see that due to randomness, the bootstrapped samples are all different although they all are of the same size. Secondly, since bootstrapped samples are different, they will have different intercept and slope estimates. In other words, all the blue fitted lines from the bootstrapped samples are different. They are also different from the red fitted line obtained from the original sample.
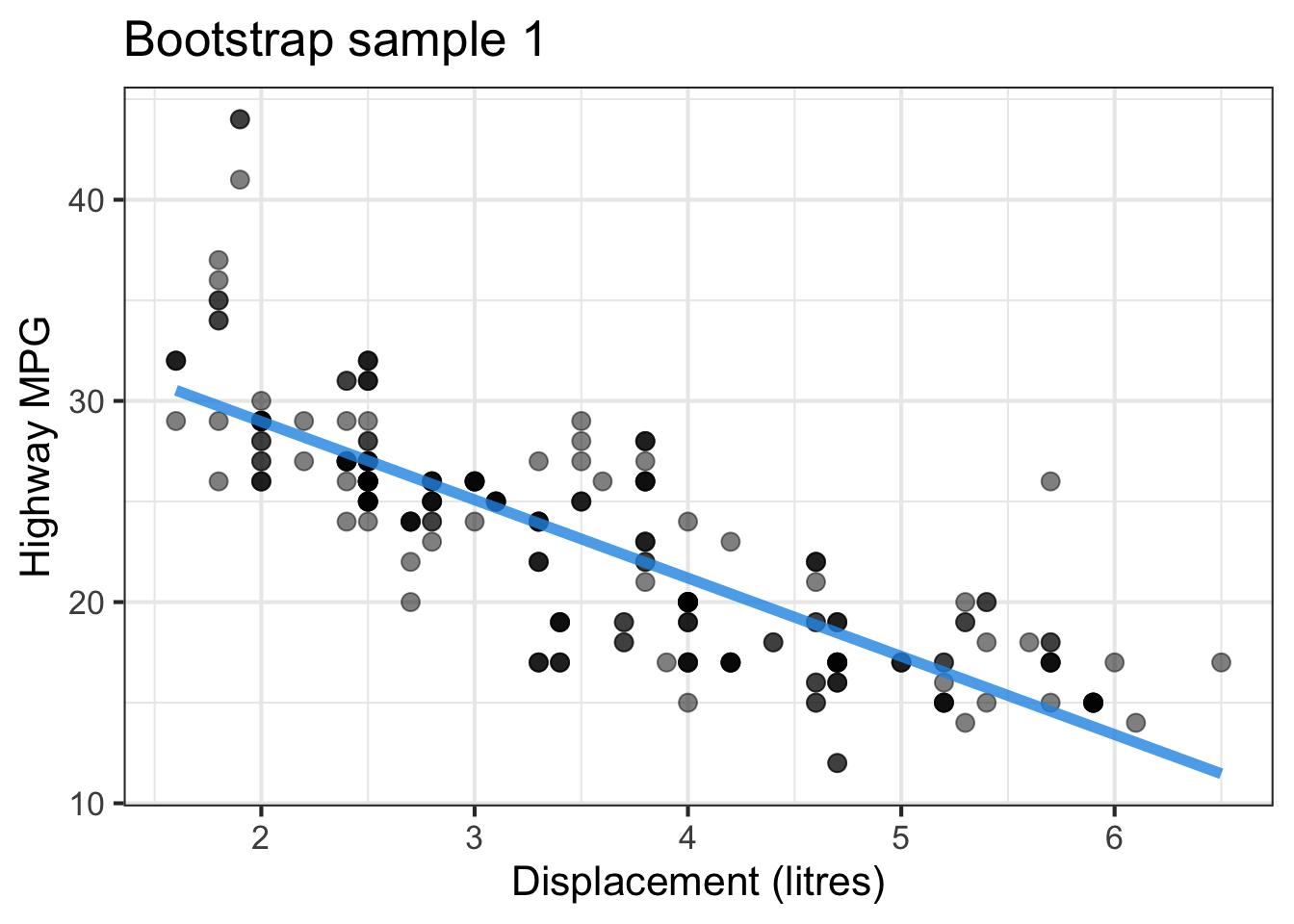
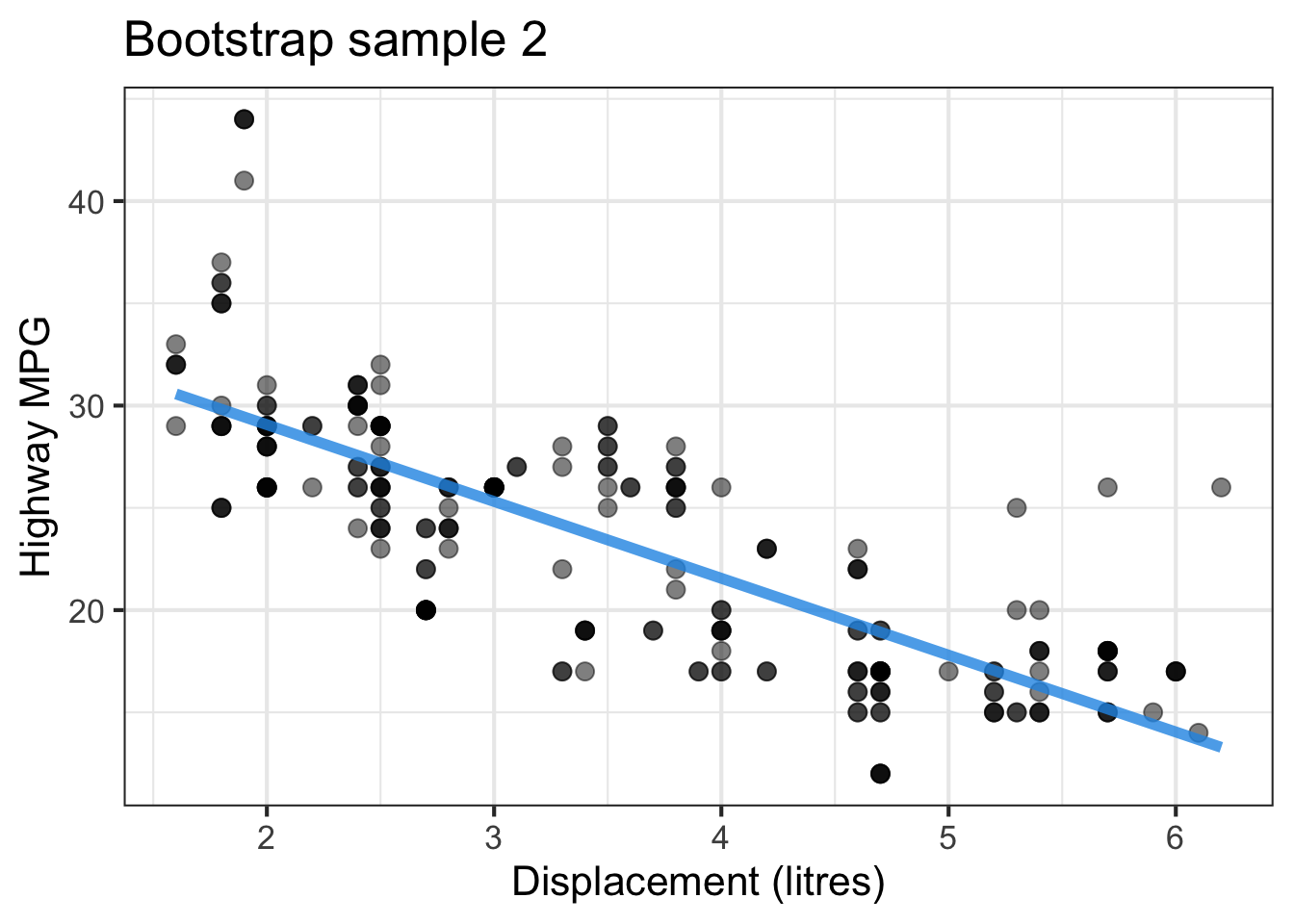
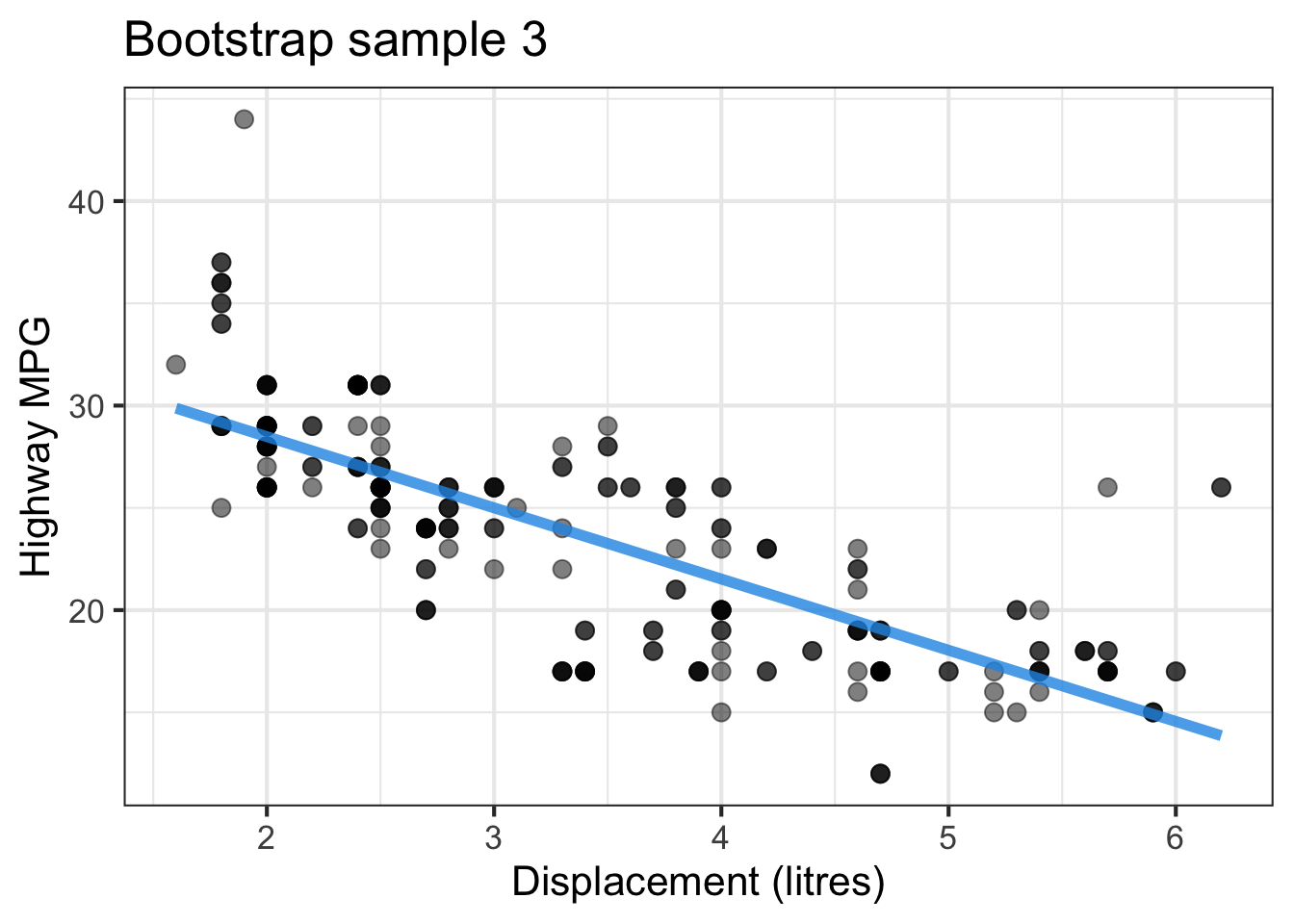
We can repeatedly create bootstrapped samples lots of times. The collection of the fitted lines or the estimated intercepts and slopes let us know their possible values and the degree of uncertainty. Same as previous inference, we find that the uncertainty about the mean response when the predictor is away from its mean is larger than the uncertainty when the predictor value is close to its mean.
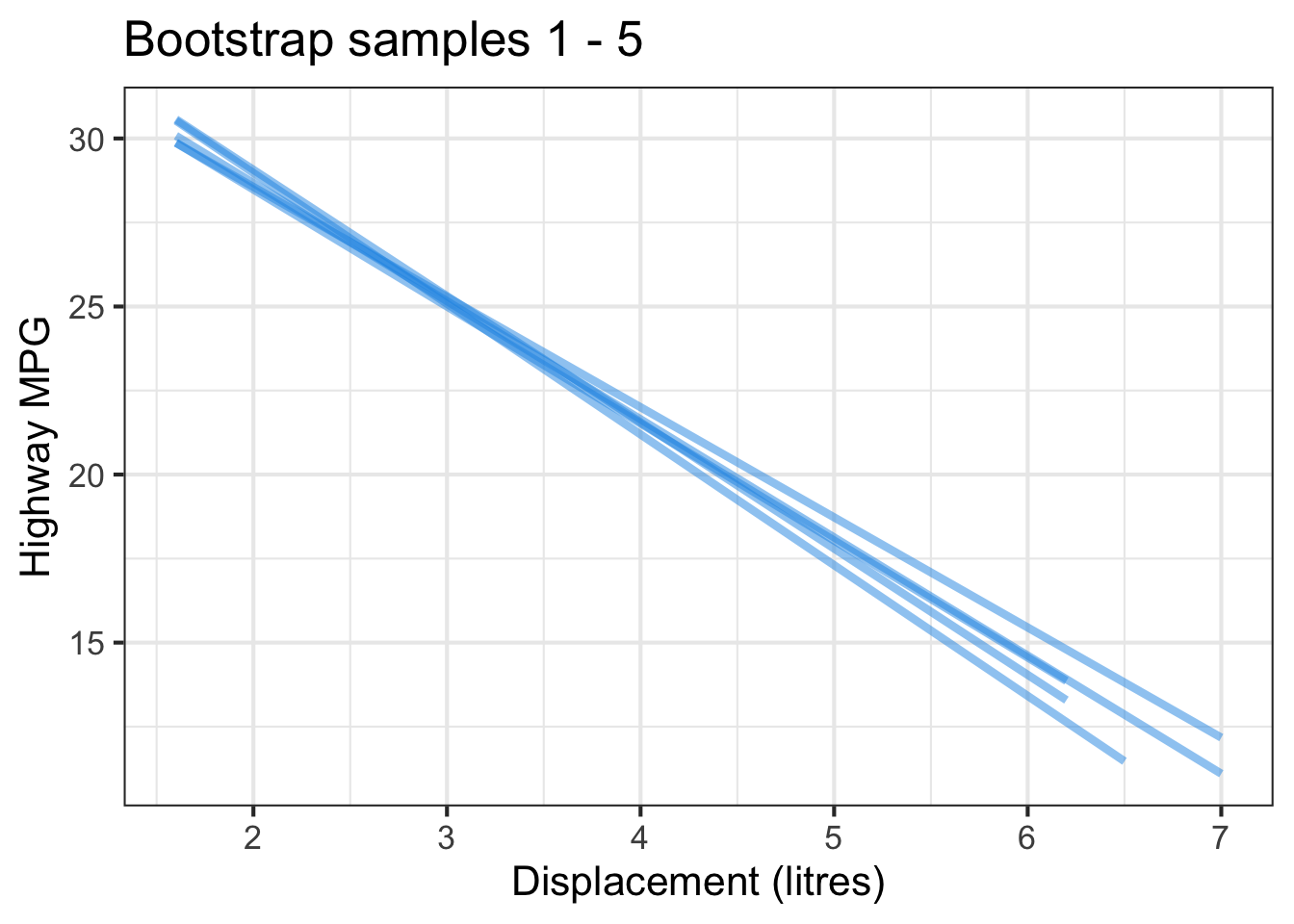
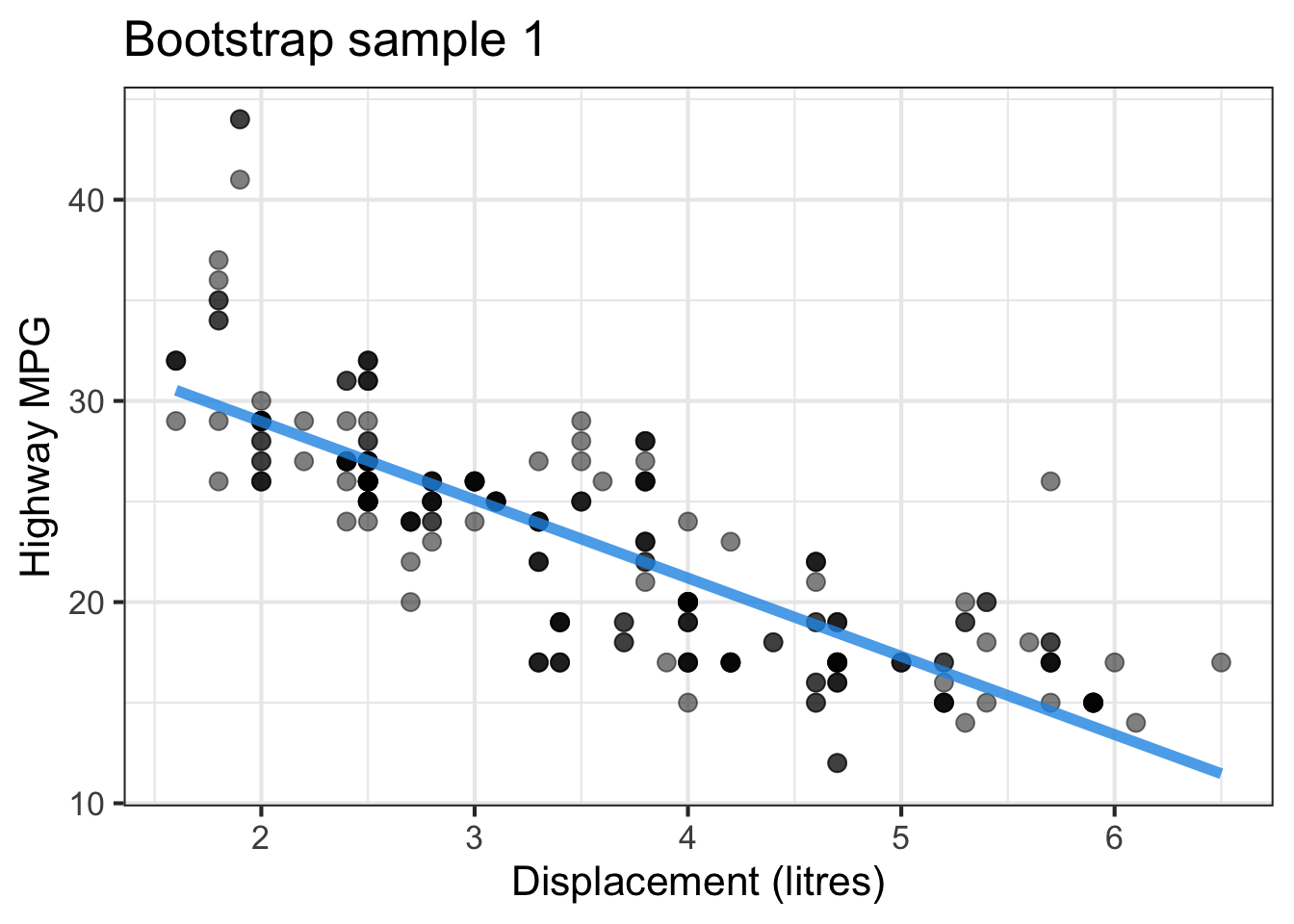
Another observation is that if we get the average of the 100 intercepts and slopes, as shown in the left panel of the figure below, the mean bootstrapped fitted line (darkblue) will be pretty close to the fitted line obtained from the original sample (red). The distribution of bootstrapped sample of slope with the mean (blue) and the 95% bootstrap CI (dashed green) is shown on the right.
As discussed in Chapter 15, we can use the boot package and its function boot() to do bootstrappingin R.
library(boot)
set.seed(2024)
coef_fn <- function(data, index) {
coef(lm(hwy ~ displ, data = data, subset = index))
}
boot_lm <- boot::boot(data = mpg, statistic = coef_fn, R = 100)
boot_lm
ORDINARY NONPARAMETRIC BOOTSTRAP
Call:
boot::boot(data = mpg, statistic = coef_fn, R = 100)
Bootstrap Statistics :
original bias std. error
t1* 35.697651 0.12574153 0.9733547
t2* -3.530589 -0.03859401 0.2745006The function coef_fn returns the regression coefficient estimates from the bootstrapped samples that are the statistics needed for the argument statistic in the boot() function. We generate 100 bootstrap samples, and 100 corresponding bootstrap intercepts and slopes. The bootstrapping result is saved in the object boot_lm which is a list. boot_lm$t0 saves the boot_lm$t saves the 100 bootstrap estimated intercepts and slopes. The bias shown in the printed output is the difference between the mean of bootstrap estimates and the original coefficient estimates. The std. error is derived from sd(boot_mean$t) that estimates the variance of the sample mean.
boot_lm$t0(Intercept) displ
35.697651 -3.530589 head(boot_lm$t) [,1] [,2]
[1,] 37.07809 -3.862234
[2,] 35.37438 -3.421966
[3,] 35.15120 -3.383944
[4,] 38.05982 -4.184231
[5,] 37.04109 -3.847217
[6,] 35.22920 -3.335708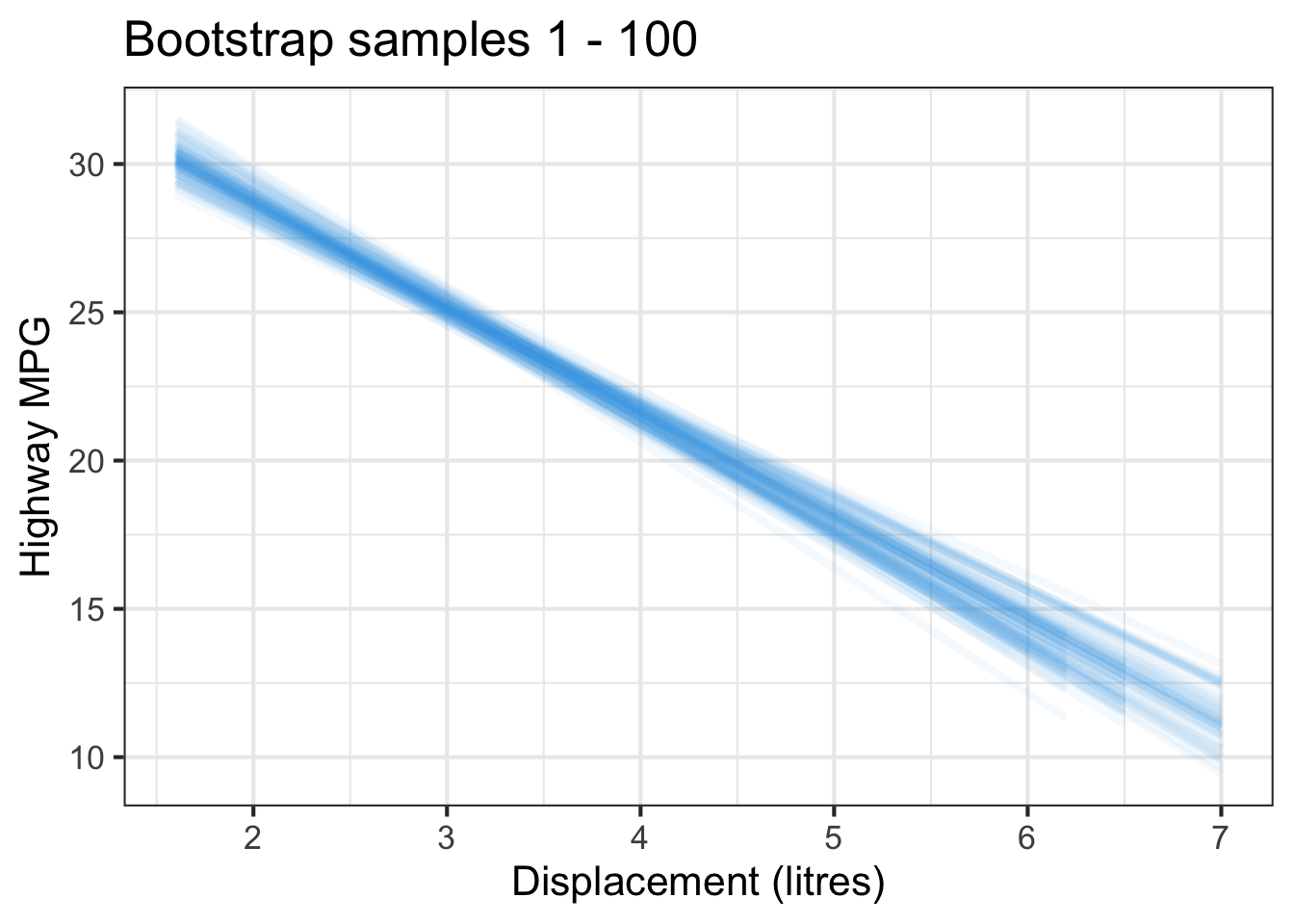
We can get the confidence intervals for intercept and slope using boot.ci() as we do in Chapter 15.
BOOTSTRAP CONFIDENCE INTERVAL CALCULATIONS
Based on 100 bootstrap replicates
CALL :
boot.ci(boot.out = boot_lm, type = c("norm", "basic", "perc"),
index = 1)
Intervals :
Level Normal Basic Percentile
95% (33.66, 37.48 ) (33.52, 37.78 ) (33.62, 37.87 )
Calculations and Intervals on Original Scale
Some basic intervals may be unstable
Some percentile intervals may be unstableBOOTSTRAP CONFIDENCE INTERVAL CALCULATIONS
Based on 100 bootstrap replicates
CALL :
boot.ci(boot.out = boot_lm, type = c("norm", "basic", "perc"),
index = 2)
Intervals :
Level Normal Basic Percentile
95% (-4.030, -2.954 ) (-4.071, -2.941 ) (-4.121, -2.990 )
Calculations and Intervals on Original Scale
Some basic intervals may be unstable
Some percentile intervals may be unstableThere are several ways of conducting bootstrapping in R. Here we choose to to use the boot package. Other popular packages include car, and infer packages of the tidymodels ecosystem. The car package is useful for regression analysis, and tidymodels is a trendy R framework of doing data science and machine learning.
To do bootstrapped regression in Python, we can use the resample() function in sklearn.utils to resample the response and predictor values in the data set with replacement. For each resmaple data, we fit the ols regression, then extract it parameter estimates. All boostrapped samples of coefficients are saved in the object boot_coefs. For better presentation, it is converted into a DataFrame.
# Bootstrapping
from sklearn.utils import resample
boot_coefs = [ols('hwy ~ displ', data=resample(mpg[['displ', 'hwy']], replace=True)).fit().params for i in range(100)]
boot_coefs = pd.DataFrame(boot_coefs)
boot_coefs.head() Intercept displ
0 37.270293 -4.029482
1 35.776571 -3.629601
2 37.064544 -3.840732
3 35.037505 -3.451112
4 36.427877 -3.839720# Histograms of bootstrap distribution
plt.figure(figsize=(12, 5))
plt.subplot(1, 2, 1)
plt.hist(boot_coefs['Intercept'])
plt.title("Bootstrap Distribution: Intercept")
plt.subplot(1, 2, 2)
plt.hist(boot_coefs['displ'])
plt.title("Bootstrap Distribution: Slope")
plt.show()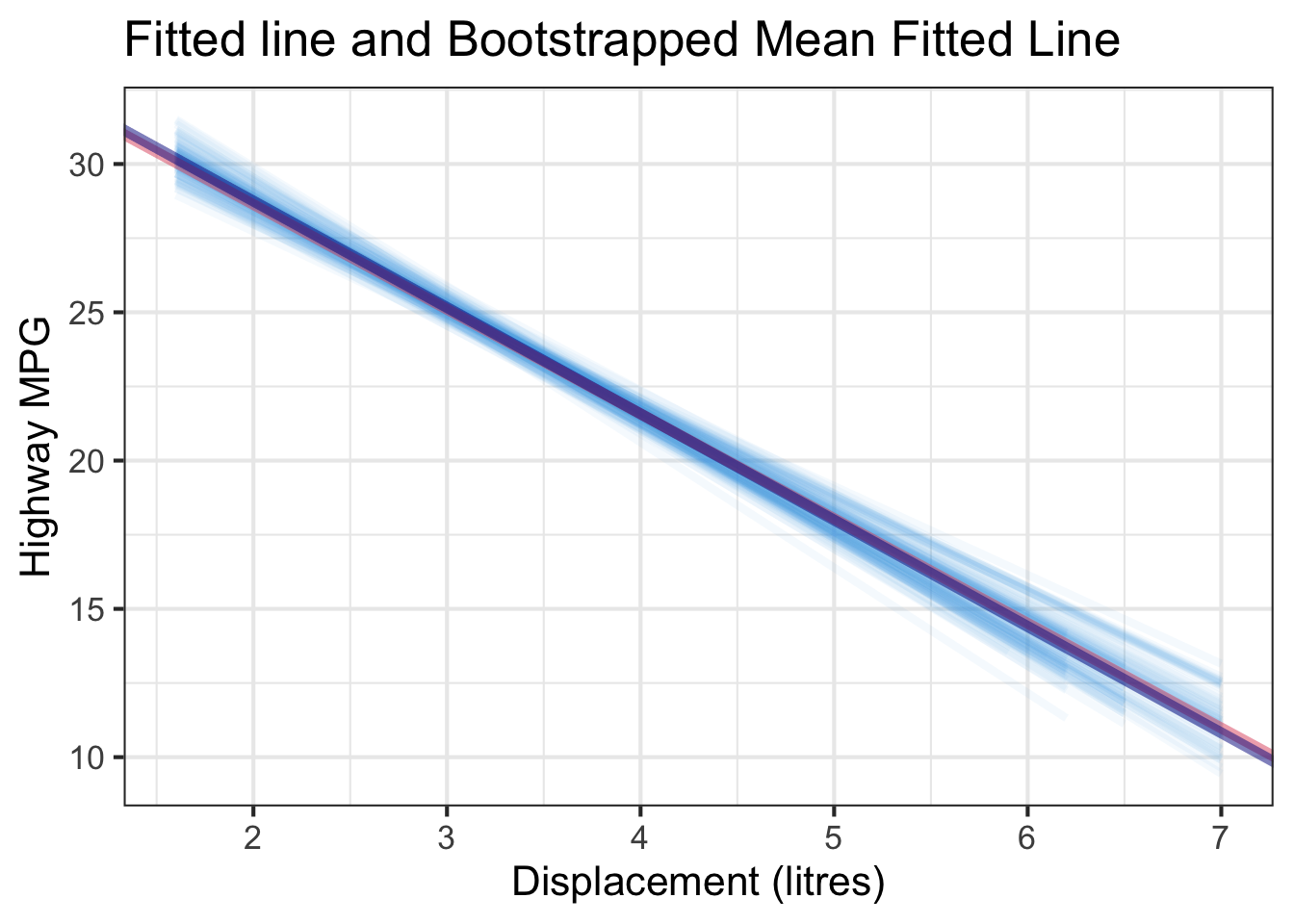
The bootstrapped confidence intervals are obtained by finding the 2.5% and 97.5% quantiles of the bootstrapped samples.
np.percentile(a=boot_coefs['Intercept'], q=[2.5, 97.5])array([34.10229532, 37.42719222])np.percentile(a=boot_coefs['displ'], q=[2.5, 97.5])array([-4.0128384 , -3.03886978])27.8 Relationship between ANOVA and Regression*
The predictor in our regression example is displ, which is a numerical variable. Remember that the regression model can also have categorical predictors. In Chapter 24, we learn the ANOVA, a model for examining whether or not the factors affect the mean response level. These factors are in fact a “value” of some categorical variable being studied. For example, when we examine the effect of different treatments (None, Fertilizer, Irrigation, Fertilizer and Irrigation) on the mean weights of poplar trees, we are examining the relationship between the two variables, the numerical response variable weight of poplar tree and the categorical explanatory variable treatment type.
In fact, when all the predictors in the regression model are categorical variables, ANOVA and regression are somewhat equivalent. Let’s first learn how to express a categorical variable in a regression model, then see why ANOVA can be viewed as a specific regression model.
27.8.1 Categorical predictors and dummy variables
Suppose now we want to see how the transmission type trans affects high miles per gallon hwy.
# A tibble: 234 × 2
hwy trans
<int> <chr>
1 29 auto(l5)
2 29 manual(m5)
3 31 manual(m6)
4 30 auto(av)
5 26 auto(l5)
6 26 manual(m5)
7 27 auto(av)
8 26 manual(m5)
9 25 auto(l5)
10 28 manual(m6)
# ℹ 224 more rows hwy trans
0 29 auto(l5)
1 29 manual(m5)
2 31 manual(m6)
3 30 auto(av)
4 26 auto(l5)
.. ... ...
229 28 auto(s6)
230 29 manual(m6)
231 26 auto(l5)
232 26 manual(m5)
233 26 auto(s6)
[234 rows x 2 columns]Note that trans has so many different categories or “values” because of the parentheses terms. We can remove them so that the trans variable only has two categories: auto and manual, where auto means automatic transmission, and manual means manual transmission. The cleaned data set is called mpg_trans.
mpg_trans[, c("hwy", "trans")]# A tibble: 234 × 2
hwy trans
<int> <chr>
1 29 auto
2 29 manual
3 31 manual
4 30 auto
5 26 auto
6 26 manual
7 27 auto
8 26 manual
9 25 auto
10 28 manual
# ℹ 224 more rowsBefore we fit a regression model, we need to make sure that the categorical variable is of type character or factor in R.
typeof(mpg_trans$trans)[1] "character"We use exactly the same command lm() to fit the regression when the predictor is categorical.
lm(hwy ~ trans, data = mpg_trans)
Call:
lm(formula = hwy ~ trans, data = mpg_trans)
Coefficients:
(Intercept) transmanual
22.293 3.486 mpg_trans[["hwy", "trans"]] hwy trans
0 29 auto
1 29 manual
2 31 manual
3 30 auto
4 26 auto
.. ... ...
229 28 auto
230 29 manual
231 26 auto
232 26 manual
233 26 auto
[234 rows x 2 columns]We use exactly the same command ols() to fit the regression when the predictor is categorical.
reg_fit_trans = ols('hwy ~ trans', data=mpg_trans).fit()
reg_fit_trans.summary()| Dep. Variable: | hwy | R-squared: | 0.076 |
| Model: | OLS | Adj. R-squared: | 0.072 |
| Method: | Least Squares | F-statistic: | 19.08 |
| Date: | Thu, 12 Jun 2025 | Prob (F-statistic): | 1.89e-05 |
| Time: | 11:50:13 | Log-Likelihood: | -739.78 |
| No. Observations: | 234 | AIC: | 1484. |
| Df Residuals: | 232 | BIC: | 1490. |
| Df Model: | 1 | ||
| Covariance Type: | nonrobust |
| coef | std err | t | P>|t| | [0.025 | 0.975] | |
| Intercept | 22.2930 | 0.458 | 48.696 | 0.000 | 21.391 | 23.195 |
| trans[T.manual] | 3.4862 | 0.798 | 4.368 | 0.000 | 1.914 | 5.059 |
| Omnibus: | 5.531 | Durbin-Watson: | 0.610 |
| Prob(Omnibus): | 0.063 | Jarque-Bera (JB): | 5.215 |
| Skew: | 0.350 | Prob(JB): | 0.0737 |
| Kurtosis: | 3.209 | Cond. No. | 2.41 |
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
reg_fit_trans.paramsIntercept 22.292994
trans[T.manual] 3.486227
dtype: float64Writing code is a piece of cake. The more important thing is how we interpret the fitted result. Here, the variable trans has 2 categories. R will choose one as the baseline level that is used to compare to other levels, in this case, the only other variable. By default, R will choose the baseline level according to the category names alphabetically. Since a comes earlier than m, R chooses auto as the baseline level.
The idea is that when we fit a regression model with a categorical variable, we are learning how the (mean) response value changes when the category changes from the baseline level to another level. Notice that in the regression output, the slope coefficient label is transmanual. It is the concatenation of the categorical variable’s name trans and the non-baseline level manual. The slope tells us the changes in hwy when the transmission is changed from auto to manual.
Mathematically the fitted regression equation is
Now the question is, how we define the value of trans variable using a dummy variable or indicator variable such as
auto and manual. Furthermore, when the dummy variable is used in regression, the baseline level is always assigned value 0.
Now we are ready to interpret our fitted regression result.
-
Slope: Cars with manual transmission are expected, on average, to be 3.49 more miles per gallon than cars with auto transmission.
- Compare baseline level (
trans = auto) to the other level (trans = manual)
- Compare baseline level (
- Intercept: Cars with auto transmission are expected, on average, to have 22.3 highway miles per gallon.
Basically, the intercept value 22.3 is the average hwy MPG for cars with auto transmission because when auto, manual transmission because when manual,
In general, when the categorical variable has
27.8.2 ANOVA as a regression model
Why ANOVA can be viewed as regression? Let’s first refresh our memory of ANOVA model.
-
-
-
-
- ANOVA is a linear model.
The assumptions of ANOVA are
-
-
In our transmission example,
Now
Does this model look like a regression model? In general, for a regression model with a categorical variable, we can write the model as
We are done! If we let
By default, the regression model assumes the treatment effect of the baseline group is zero. Therefore
27.9 Exercises
Use the data in the table below to answer questions 1-7.
| Tar | 24 | 28 | 21 | 23 | 20 | 22 | 20 | 25 | ||
| Nicotine | 1.6 | 1.7 | 1.2 | 1.4 | 1.1 | 1.0 | 1.3 | 1.2 |
Construct a scatterplot using tar for the
Let
What percentage of the variation in nicotine can be explained by the linear correlation between nicotine and tar?
The Raleigh brand king size cigarette is not included in the table, and it has 21 mg of tar. What is the best predicted amount of nicotine? How does the predicted amount compare to the actual amount of 1.2 mg of nicotine? What is the value of residual?
Perform the test
Provide 95% confidence interval for
Generate the ANOVA table for the linear regression.
-
Correlation (30 points): Match each correlation to the corresponding scatterplot.
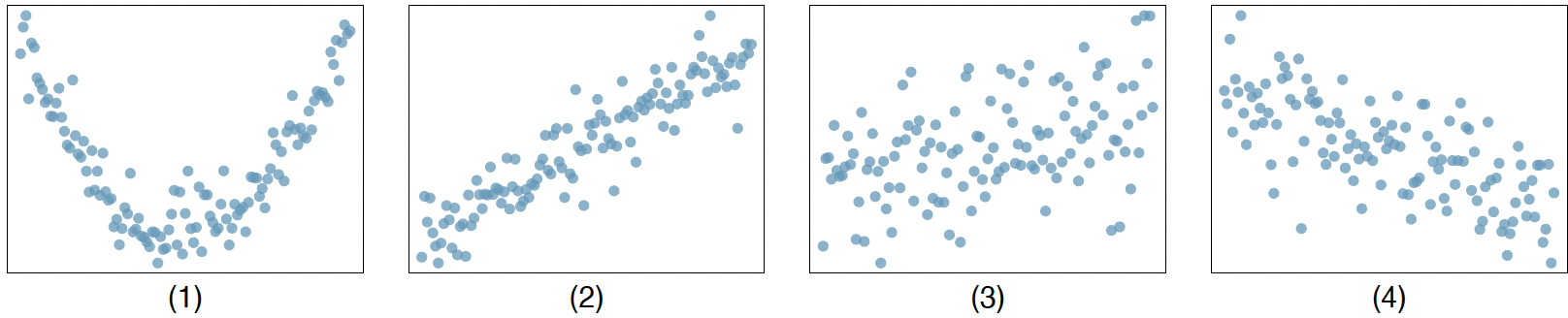
-
Regression (30 points): The following regression output is for predicting the heart weight (in g) of cats from their body weight (in kg).
- Write out the simple linear regression equation.
- Which one is the response variable and which one is the predictor (explanatory variable)?
- Interpret the slope and intercept.
| (Intercept) | -0.346 |
| body wt | 3.953 |
The random variables
We could use another definition of “the best”, for example the sum of absolute value of residuals. But the sum of squared residuals is the most commonly used one.↩︎