28 Multiple Linear Regression*
When more than one predictors are considered and put in a regression model, we are dealing with multiple linear regression. Multiple linear regression (MLR) is pretty similar to simple linear regression (SLR). They share the same idea and concept in terms of prediction and inference.
28.1 Why Multiple Regression?
The first question you may ask is why we want to use multiple regression? In practice, we often have more than one predictor in a given study, and our target response may be affected by several factors. For example, how amount of money spent on advertising on different media affect the total sales of some product? We may need more than one predictors because usually companies will spend money on several different media, not just one.
Data: total sales
We want to predict sales based on the three advertising expenditures and see which medium is more effective.
Total sales


- Predict sales based on the three advertising expenditures and see which medium is more effective.
You may wonder, how about we just fit three separate simple linear regression models, one for each predictor. Yes, we could do that. And if we do this, we’ll see that, as shown in the figure below, advertising on the 3 media is valuable because the more the money we put in, the higher sales of products we’ll get. However, fitting a separate SLR model for each predictor is not satisfactory. Let’s see why.
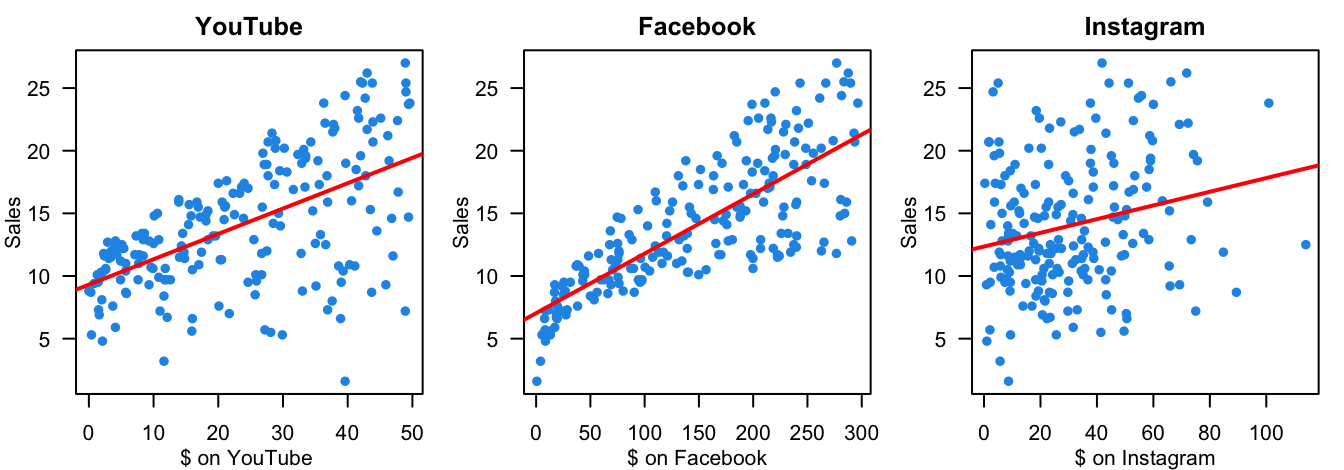
- 👉 How to make a single prediction of sales given levels of the 3 advertising media budgets?
-
How to predict the sales when the amount spent on YT is 50, 100 on FB and 30 on IG?
It is unclear how to make a single prediction of sales given levels of the three advertising media budgets, since each of the budgets is associated with a separate regression equation.
-
- 👉 Each regression equation ignores the other 2 media in forming coefficient estimates.
The effect of FB advertising on sales may be increased or decreased when YT and IG advertising are in the model.
-
IG advertising may have no impact on sales when YT and FB advertising are in the model.
If the three media budgets are correlated with each other, this can lead to very misleading estimates of the individual media effects on sales.
- 👍👍 Better approach: extend the SLR model so that it can directly accommodate multiple predictors.
I hope you don’t feel…

What I hope is…

28.2 Multiple Linear Regression (MLR) Model
Suppose we have
In the advertising example,
The model assumptions are same same as SLR that
Given the training sample data
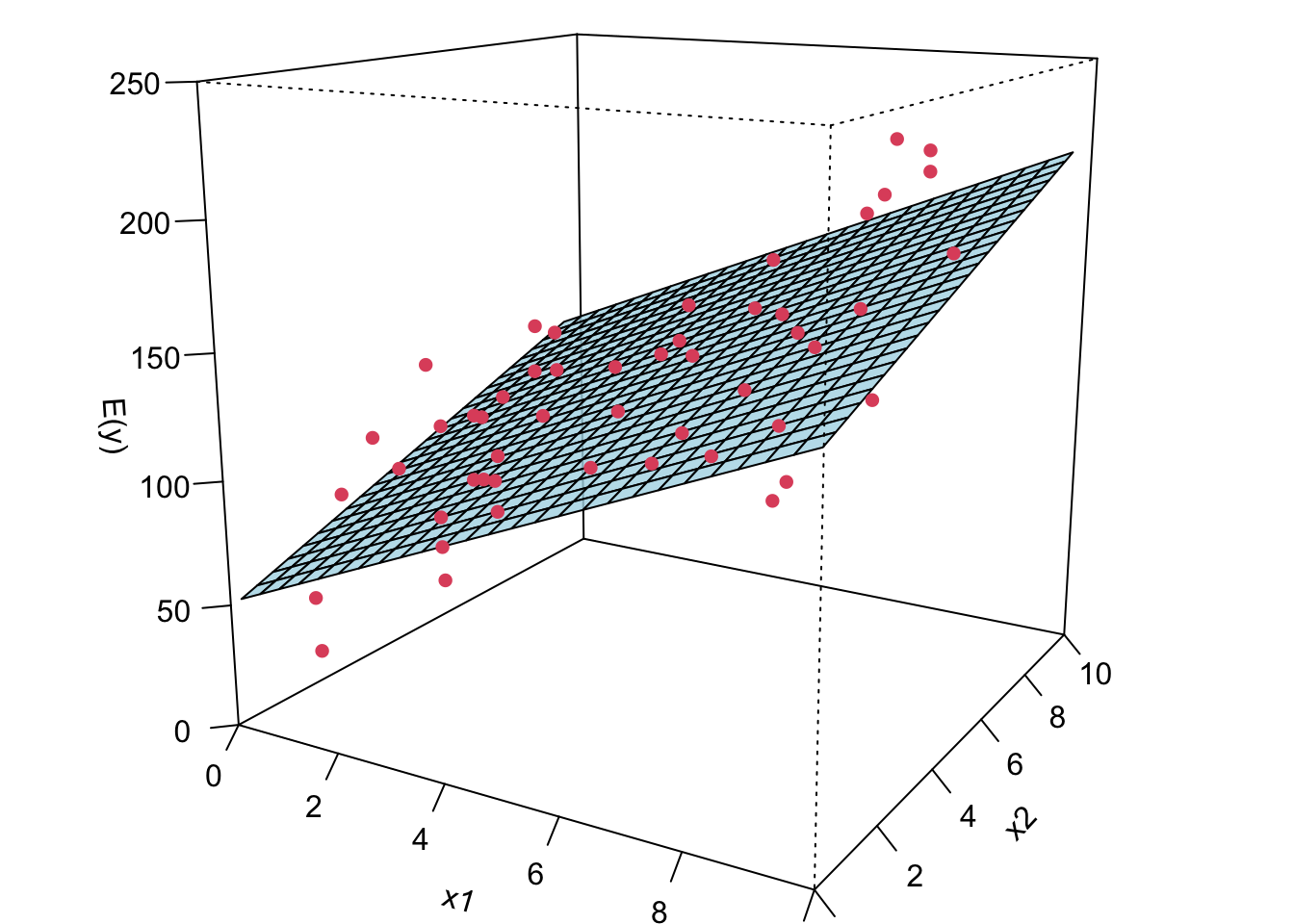
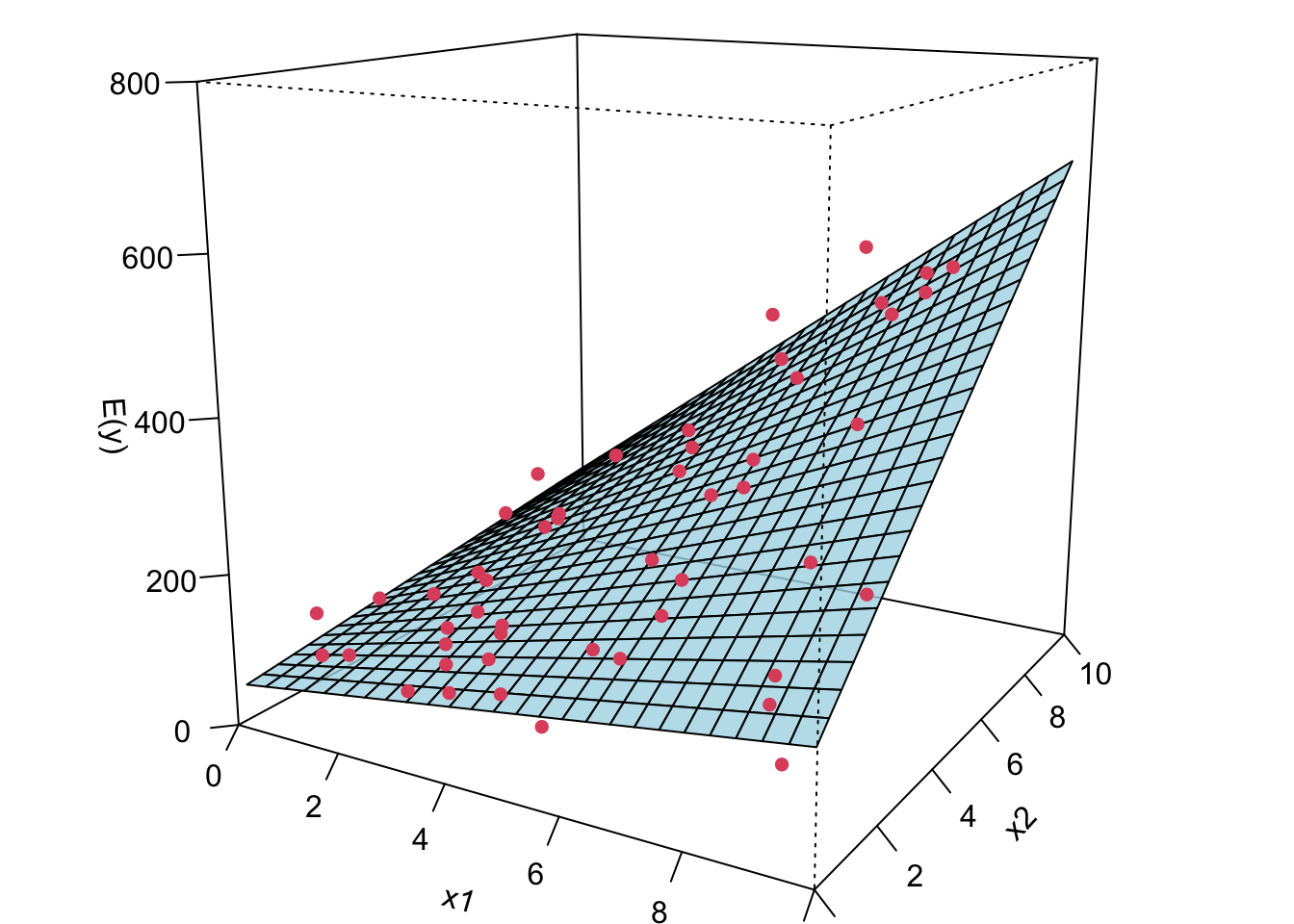
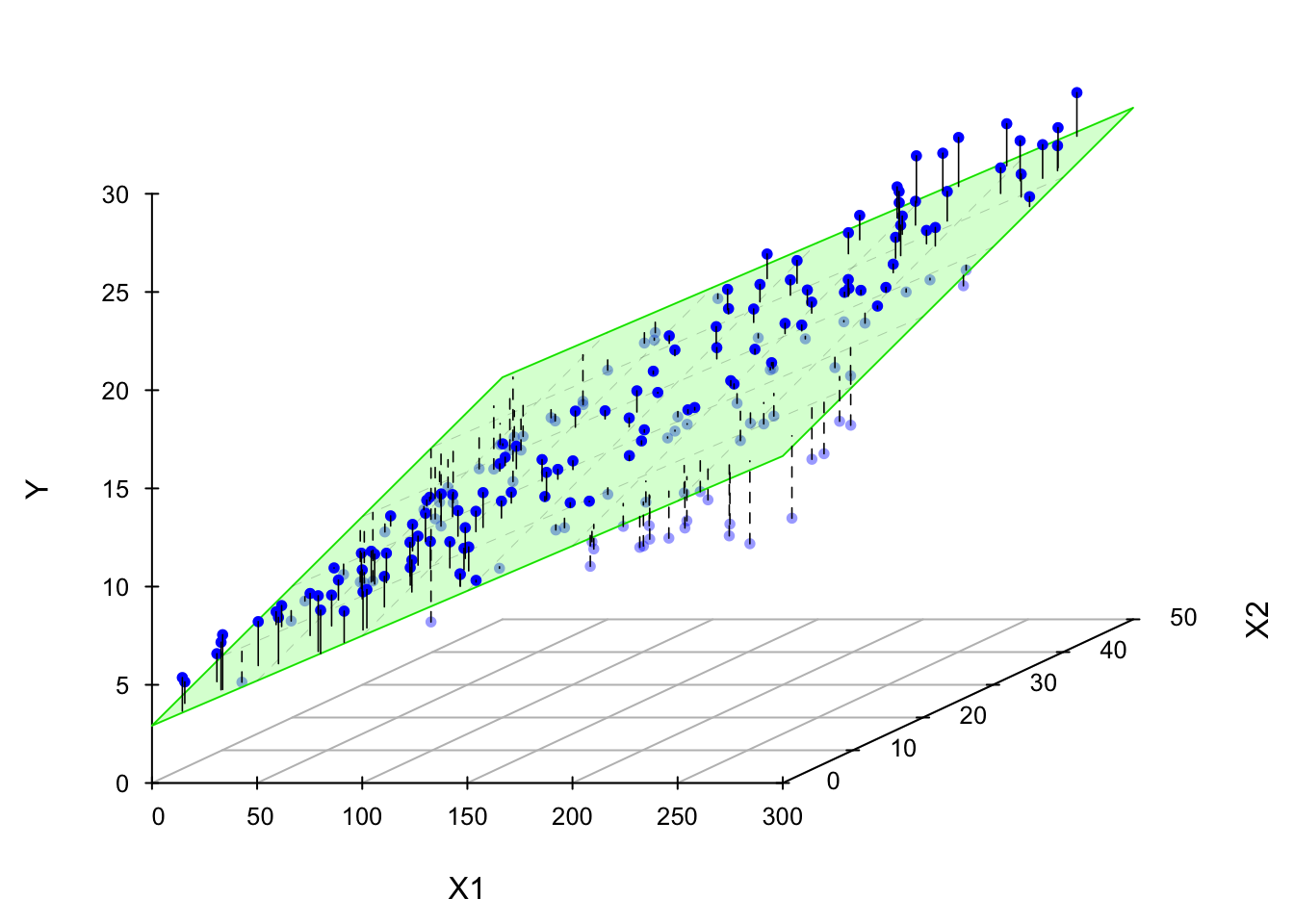
Now I’m gonna show you what a MLR looks like when we fit it to the data. If we have two predictors, we will have a sample regression plane. If we have more than two predictors in the model, we are not able to visualize it, but the idea is the same. We will have something called hyperplane or response surface that basically play the same role as the regression plane in 2D or regression line in 1D.
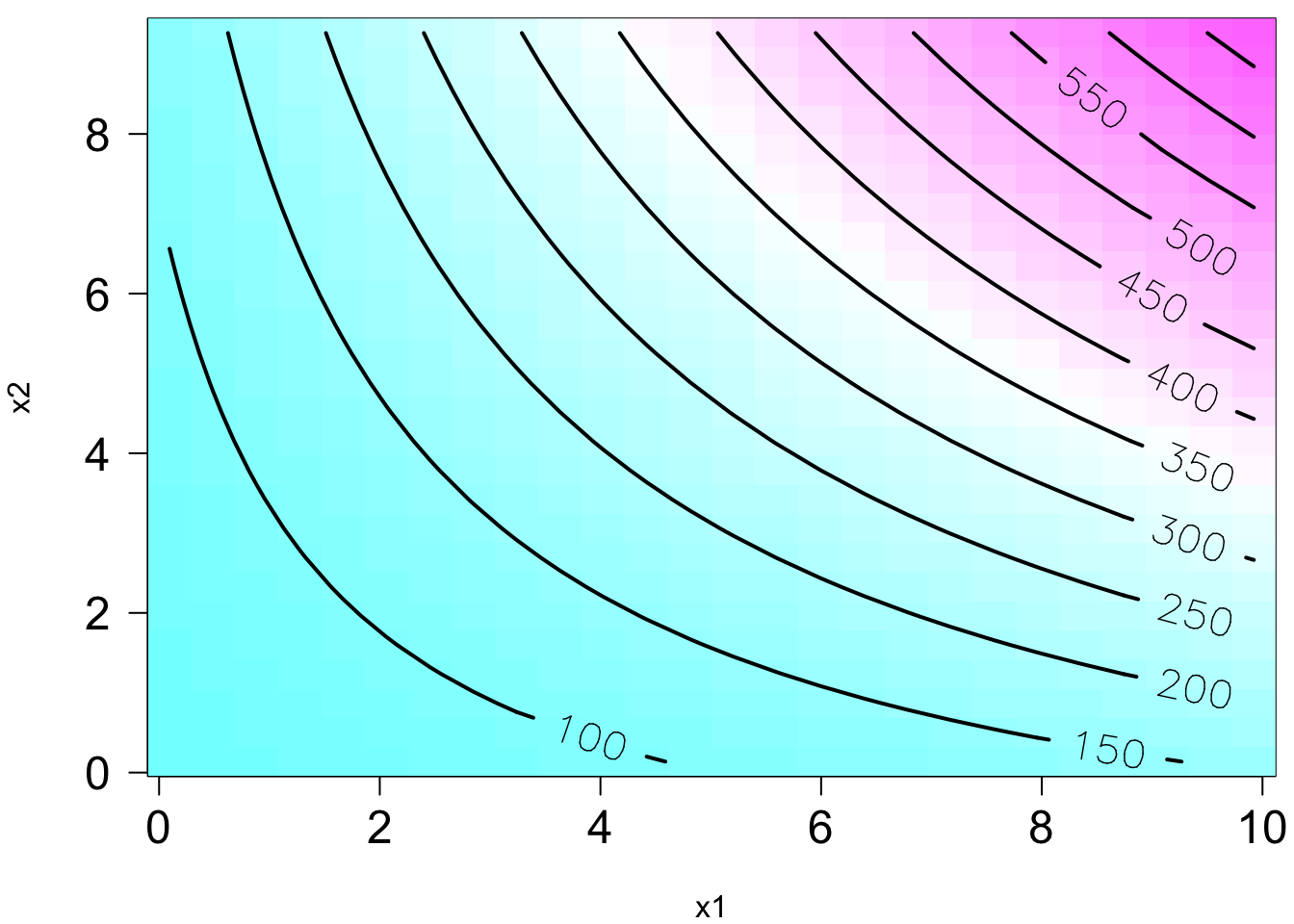
The plot on the right is the contour plot when we project the plot onto the
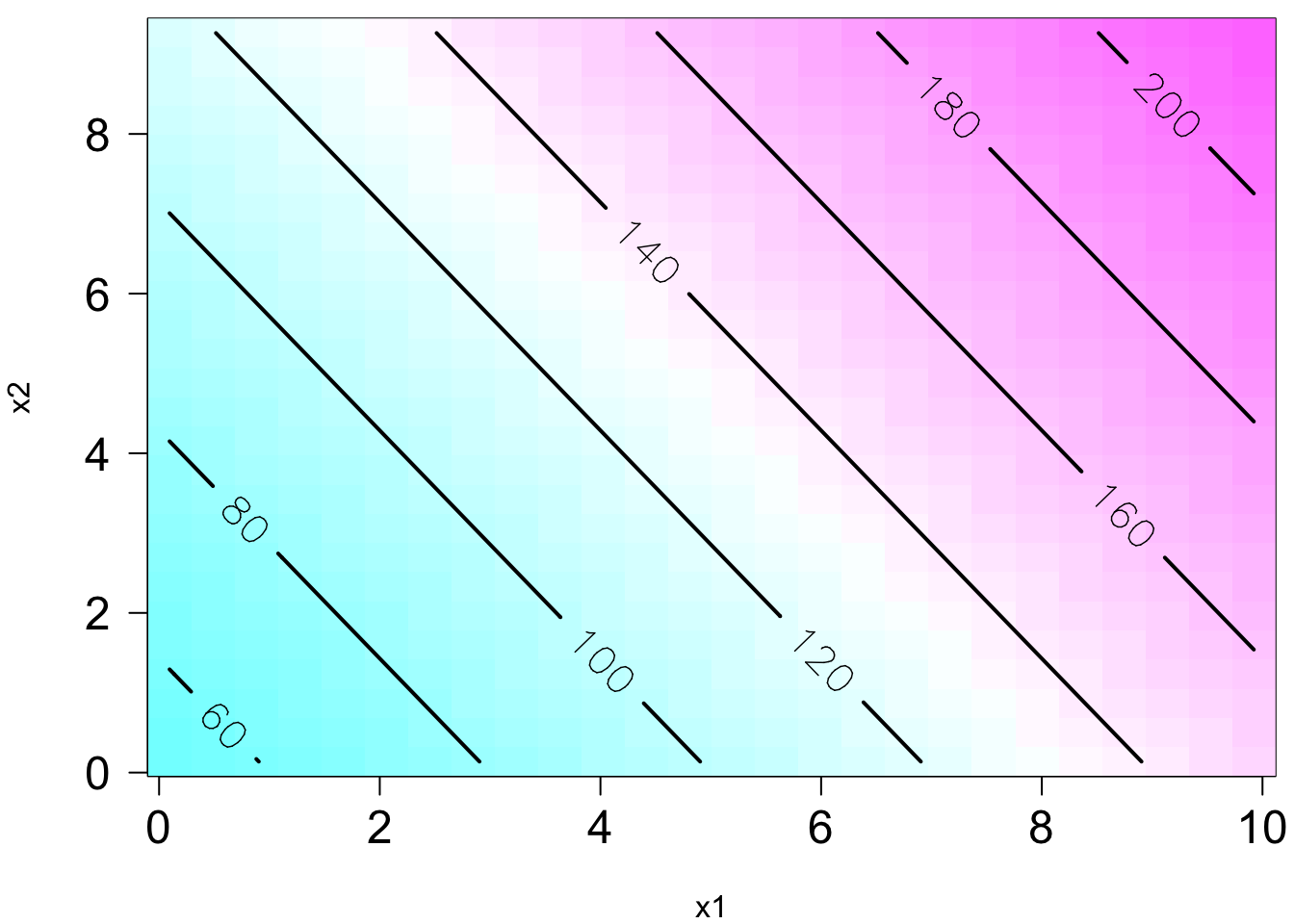
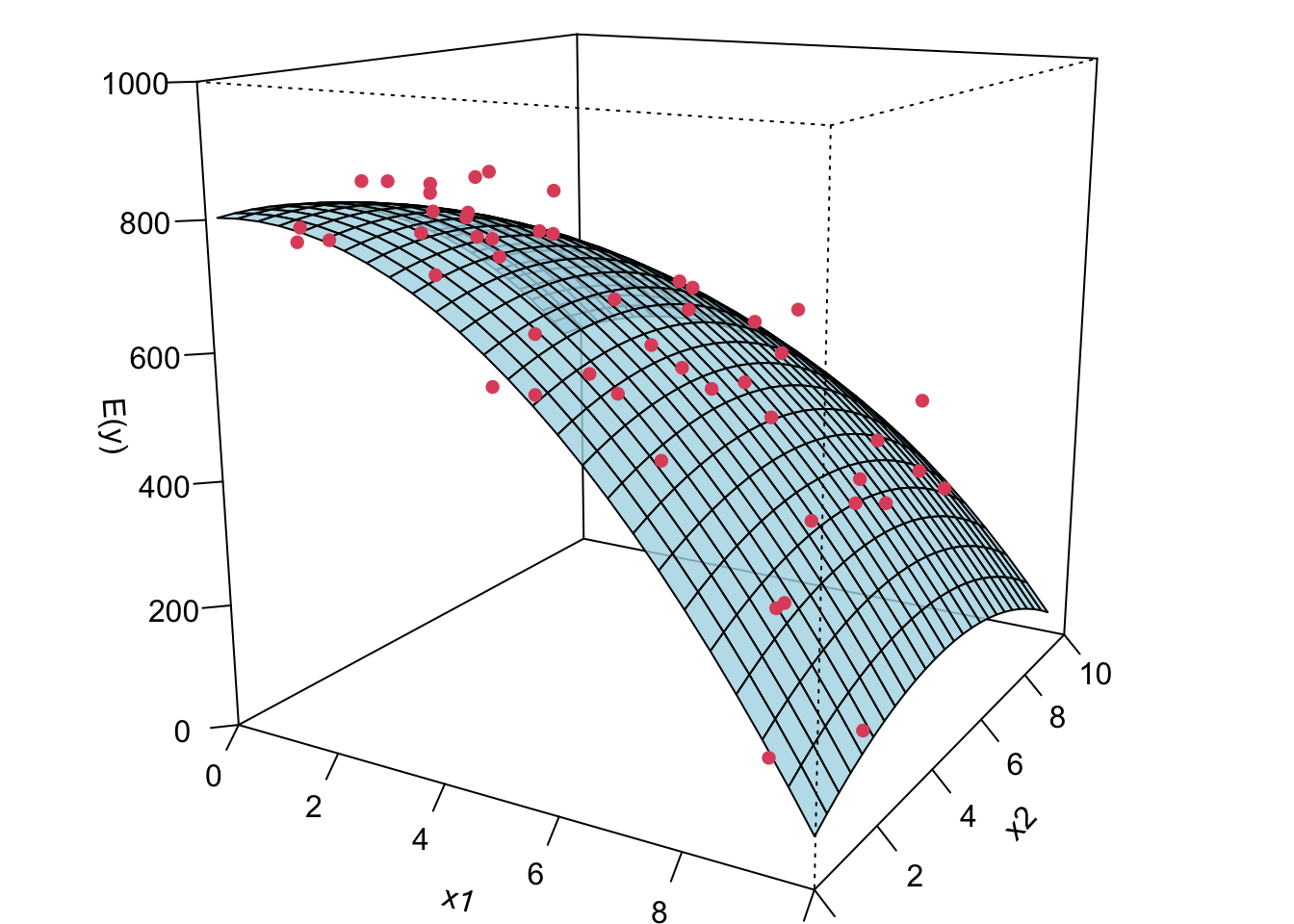
Remember in SLR, we can have a liner model that describes a nonlinear relationship. Same in MLR. We can have a linear model that generates a nonlinear response surface!
- This is in fact a linear regression model: let
- 😎 🤓 A linear model generates a nonlinear response surface!
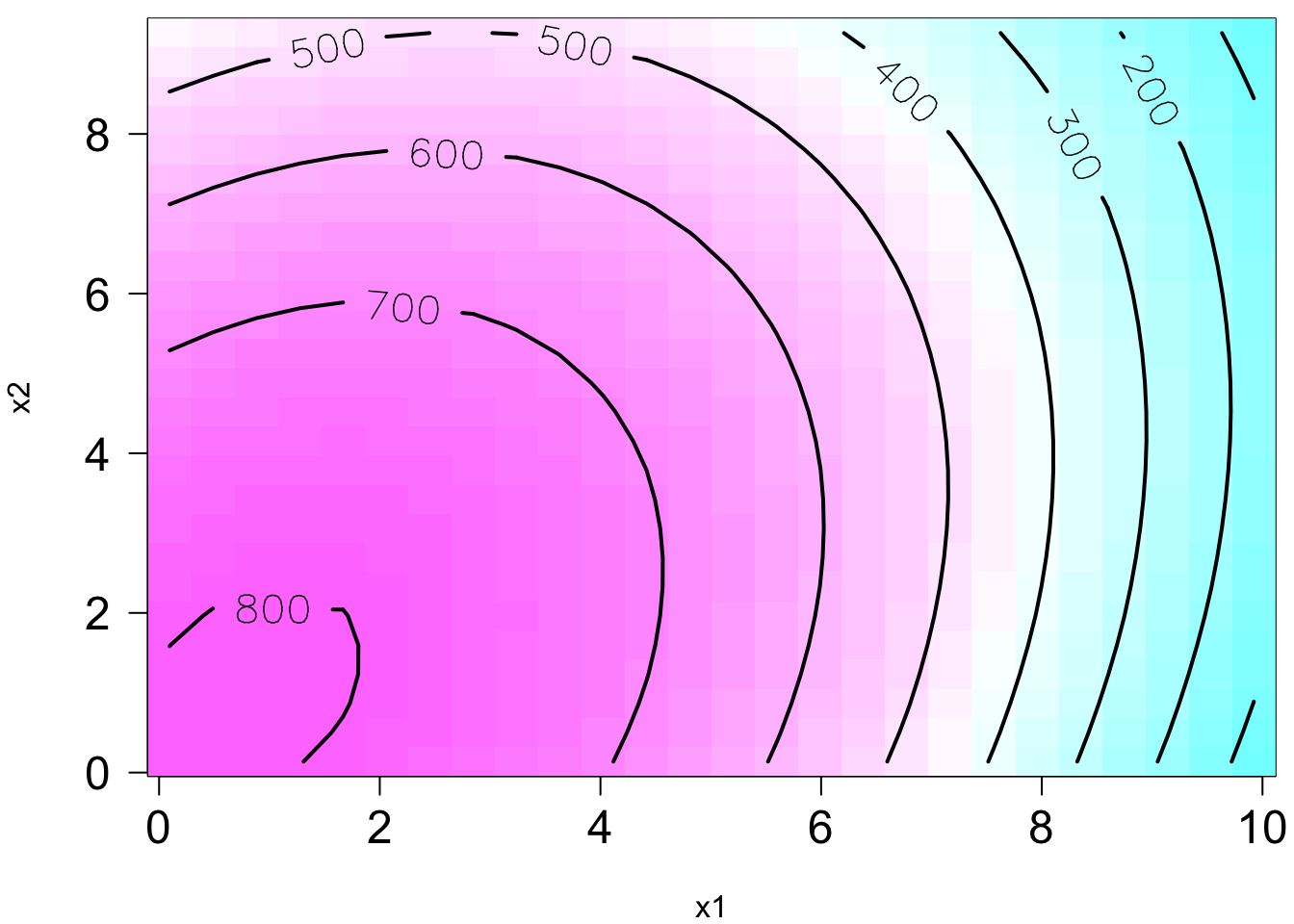
😎 🤓 A linear regression model can describe a complex nonlinear relationship between the response and predictors! The following is a 2nd order model with interaction.
28.3 Estimation of Model Parameters
28.3.1 Least Squares Estimation (LSE)
As SLR, we can define the least-squares function as the sum of squares of epsilon. The least-squares function is
We are going to choose the sample statistics
If we look at the geometry of least squares estimation of MLR, we have a visualization like this. Again, in SLR, different
Again similar to SLR, we can take derivative w.r.t
Based on the MLR model and assumptions, the LS estimator
Linear : Each
Unbiased : Each
Best : Each
Example: Least Squares Estimation
In this chapter, we use Delivery Time Data of Example 3.1 from Introduction to Linear Regression Analysis, 6th edition to demo MLR.
# Load the data set
delivery <- read.csv(file = "./data/data-ex-3-1.csv", header = TRUE)
delivery_data <- delivery[, -1]
colnames(delivery_data) <- c("time", "cases", "distance")
delivery_data time cases distance
1 16.7 7 560
2 11.5 3 220
3 12.0 3 340
4 14.9 4 80
5 13.8 6 150
6 18.1 7 330
7 8.0 2 110
8 17.8 7 210
9 79.2 30 1460
10 21.5 5 605
11 40.3 16 688
12 21.0 10 215
13 13.5 4 255
14 19.8 6 462
15 24.0 9 448
16 29.0 10 776
17 15.3 6 200
18 19.0 7 132
19 9.5 3 36
20 35.1 17 770
21 17.9 10 140
22 52.3 26 810
23 18.8 9 450
24 19.8 8 635
25 10.8 4 150import pandas as pd
delivery_data = pd.read_csv('./data/delivery_data.csv')
delivery_data time cases distance
0 16.68 7 560
1 11.50 3 220
2 12.03 3 340
3 14.88 4 80
4 13.75 6 150
5 18.11 7 330
6 8.00 2 110
7 17.83 7 210
8 79.24 30 1460
9 21.50 5 605
10 40.33 16 688
11 21.00 10 215
12 13.50 4 255
13 19.75 6 462
14 24.00 9 448
15 29.00 10 776
16 15.35 6 200
17 19.00 7 132
18 9.50 3 36
19 35.10 17 770
20 17.90 10 140
21 52.32 26 810
22 18.75 9 450
23 19.83 8 635
24 10.75 4 150Goal: fit a MLR model
Always get to know your data set before you fit any statistical or machine learning model to the data.
Each plot shows the relationship between a pair of variables.
pairs(delivery_data)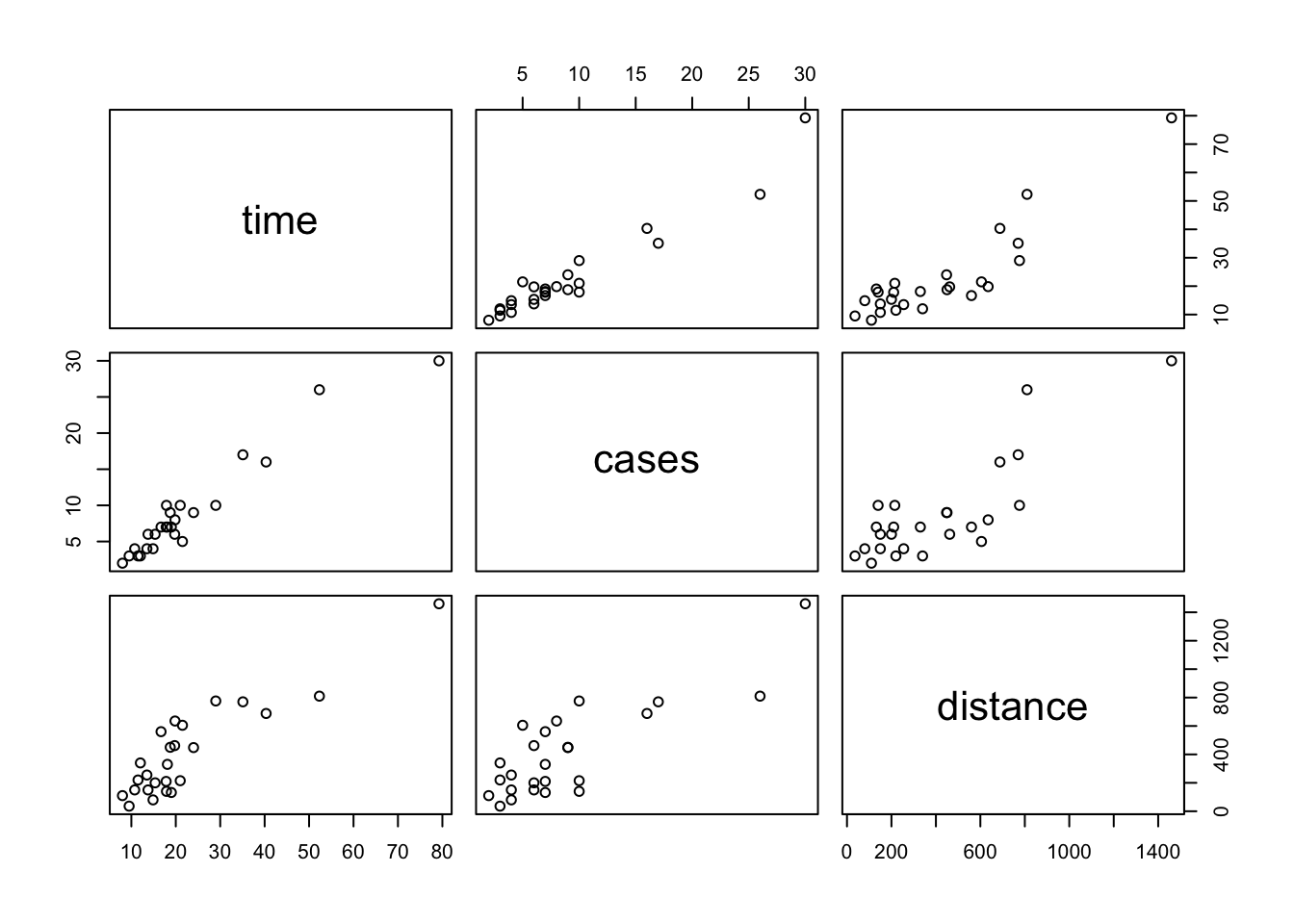
Sometimes a 3D scatterplot is useful in visualizing the relationship between the response and the regressors when there are only two regressors.
Code
par(mgp = c(2, 0.8, 0), las = 1, mar = c(4, 4, 0, 0))
library(scatterplot3d)
scatterplot3d(x = delivery_data$cases, y = delivery_data$distance, z = delivery_data$time,
xlab ="cases", ylab = "distance", zlab = "time",
xlim = c(2, 30), ylim = c(36, 1640), zlim = c(8, 80),
box = TRUE, color = "blue", mar = c(3, 3, 0, 2), angle = 30, pch = 16)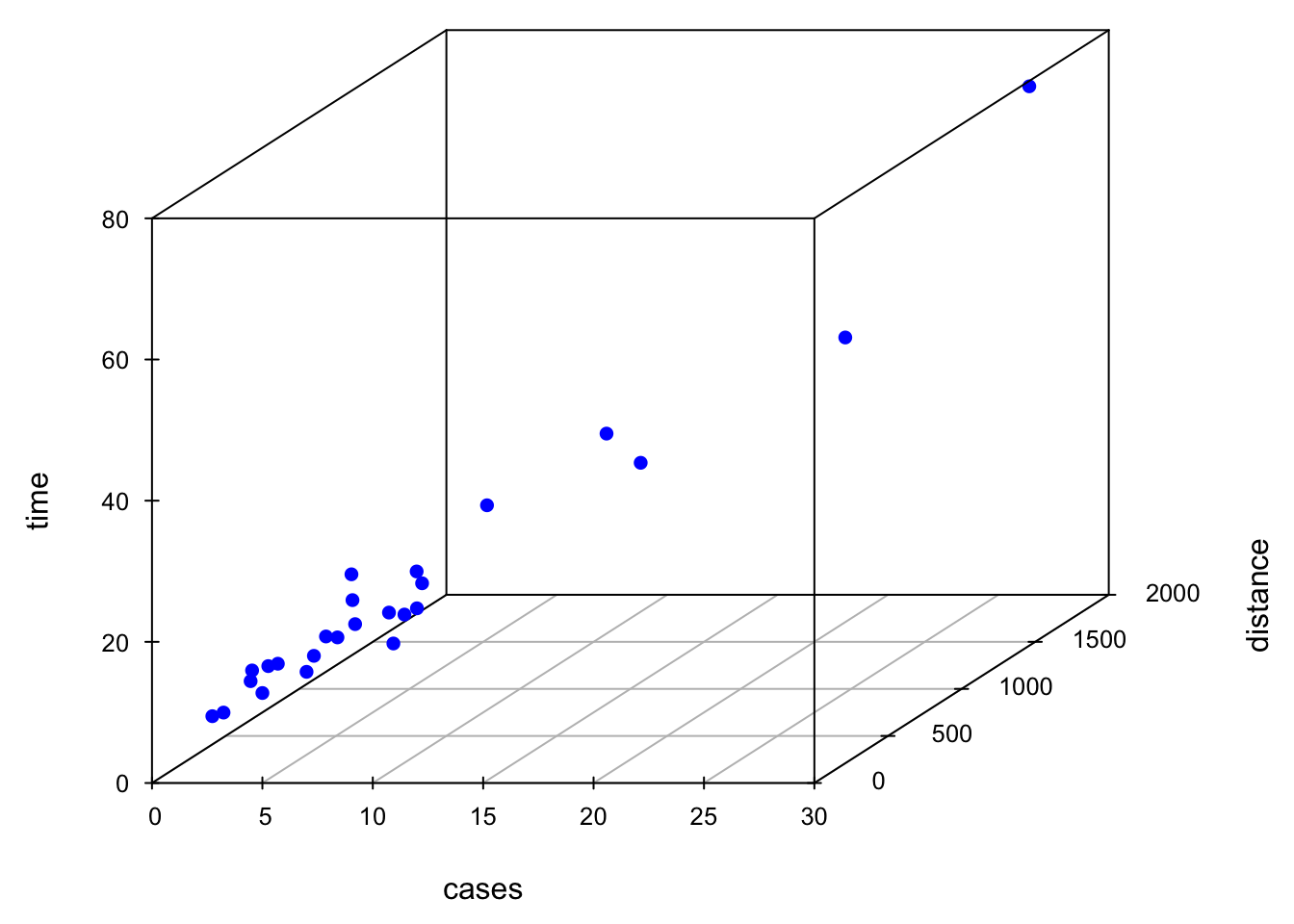
To fit the MLR model, we again use lm(). In the furmula argument, we use + to add predictors. coef(delivery_lm) or delivery_lm$coef can be used to grab the LS estimates of coefficients.
import matplotlib.pyplot as plt
pd.plotting.scatter_matrix(delivery_data, figsize=(8, 8))array([[<Axes: xlabel='time', ylabel='time'>,
<Axes: xlabel='cases', ylabel='time'>,
<Axes: xlabel='distance', ylabel='time'>],
[<Axes: xlabel='time', ylabel='cases'>,
<Axes: xlabel='cases', ylabel='cases'>,
<Axes: xlabel='distance', ylabel='cases'>],
[<Axes: xlabel='time', ylabel='distance'>,
<Axes: xlabel='cases', ylabel='distance'>,
<Axes: xlabel='distance', ylabel='distance'>]], dtype=object)plt.show()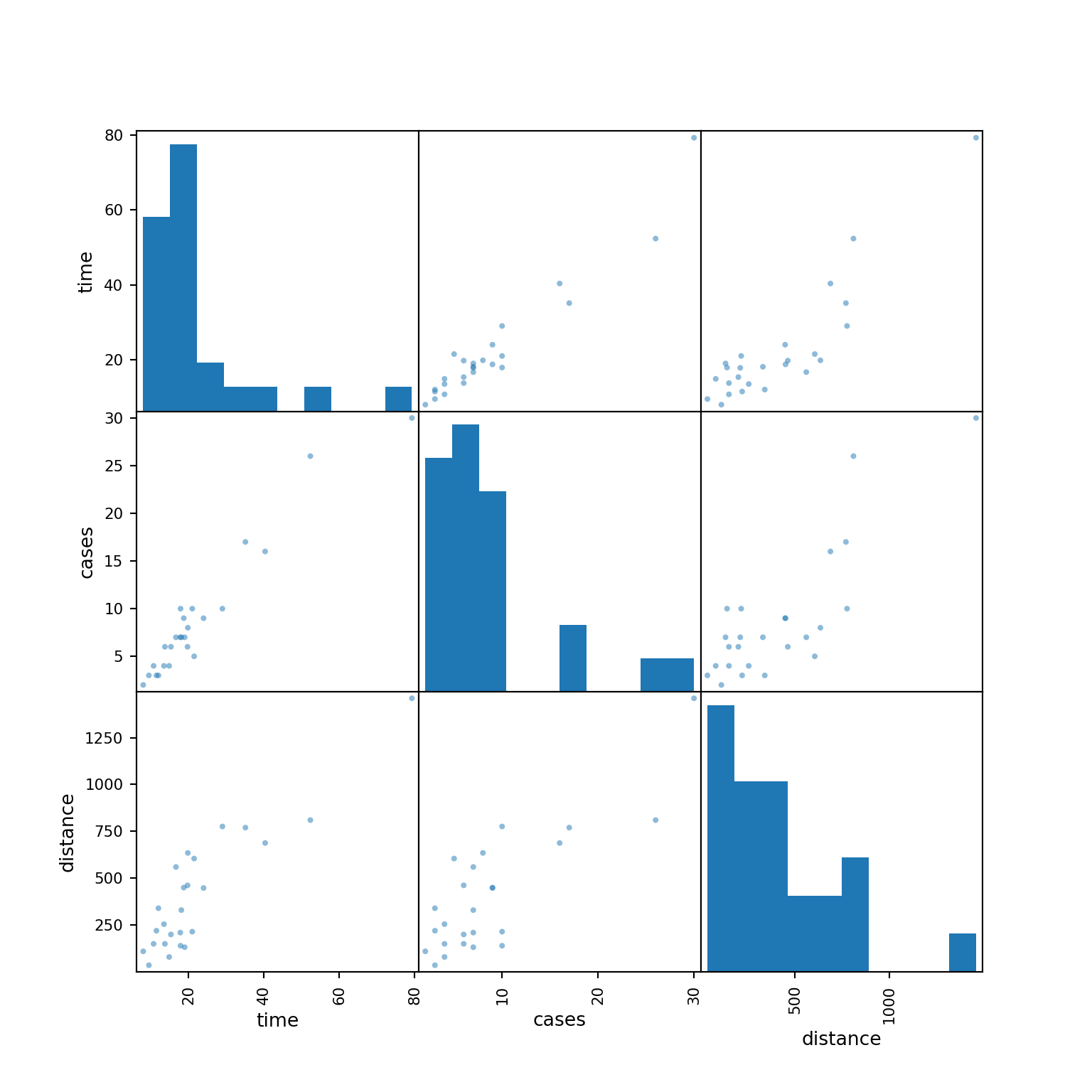
Sometimes a 3D scatterplot is useful in visualizing the relationship between the response and the regressors when there are only two regressors.
Code
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.scatter(delivery_data['cases'],
delivery_data['distance'],
delivery_data['time'])
ax.set_xlabel('Cases')
ax.set_ylabel('Distance')
ax.set_zlabel('Time')
plt.show()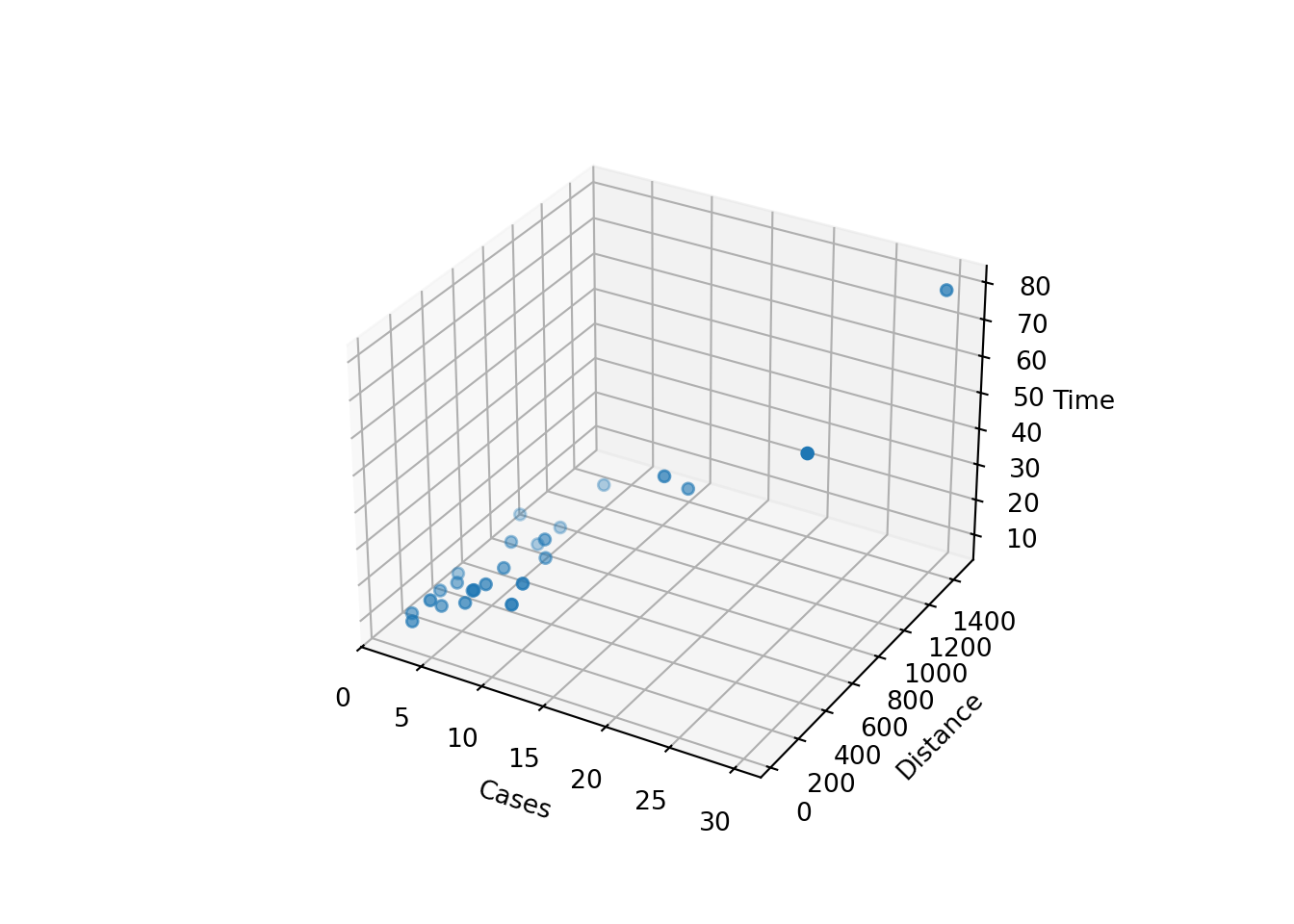
To fit the MLR model, we again use ols(). In the furmula argument, we use + to add predictors. delivery_ols.params can be used to grab the LS estimates of coefficients.
from statsmodels.formula.api import ols
delivery_ols = ols(formula='time ~ cases + distance', data=delivery_data).fit()
delivery_ols.paramsIntercept 2.341231
cases 1.615907
distance 0.014385
dtype: float64There is another function OLS() that takes response vector y and design matrix X as input arguments to fit the linear regression model.
import statsmodels.api as sm
X = delivery_data[['cases', 'distance']]
X = sm.add_constant(X) # Adds a constant term to the predictor
y = delivery_data['time']
delivery_OLS = sm.OLS(y, X).fit()
When we interpret slopes or the effect of any predictor on the response in MLR, for example,
For regression we usually don’t pay much attention to
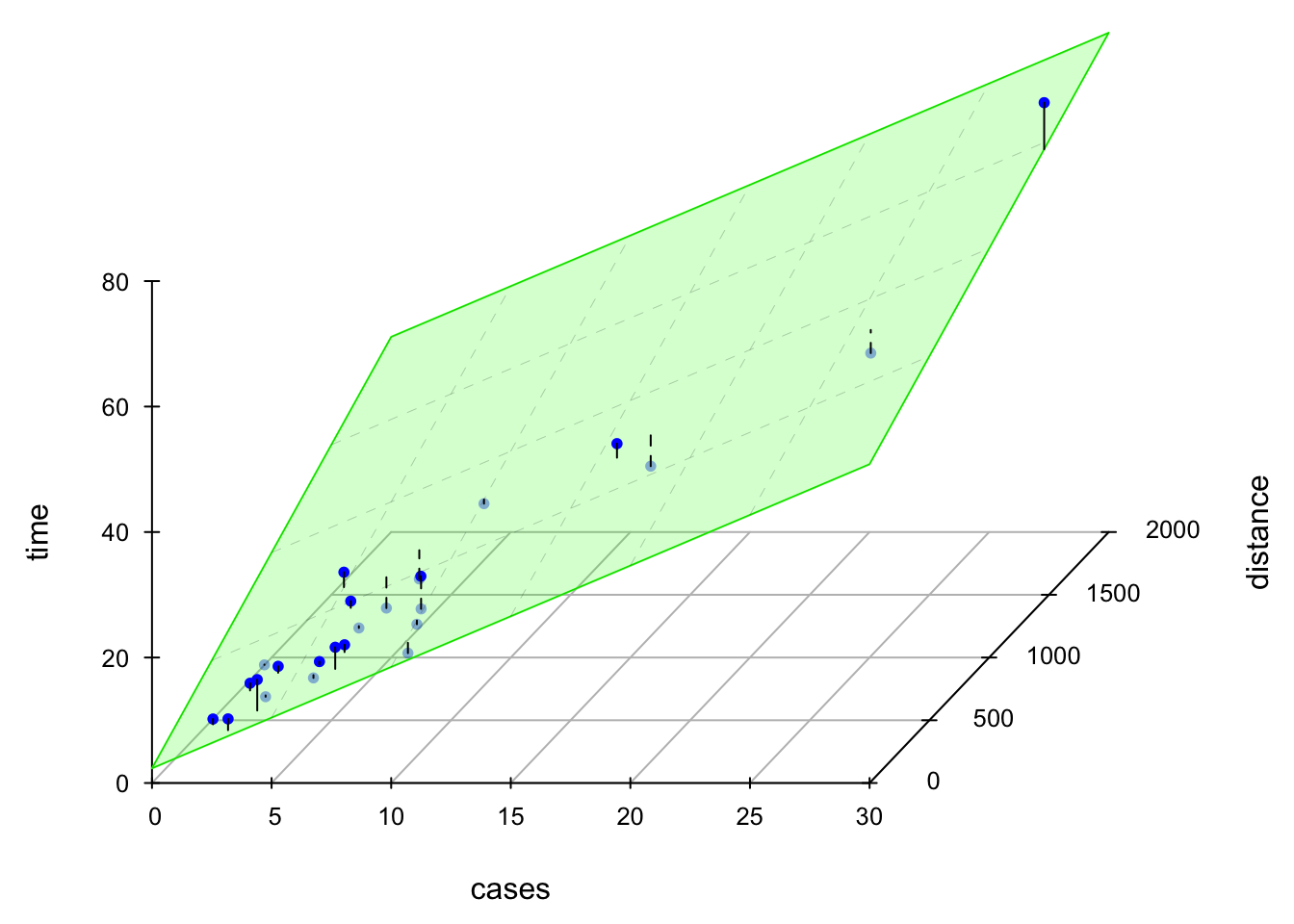
The LS fitted regression plane is shown below.
28.3.2 Estimation of
Same as SLR, the estimate of
Remember that the sum of squares residual is
Example: Estimation of
Here I show three methods to obtain the sigma that is Residual standard error: 3.26 on 22 degrees of freedom
## method 1
summ_delivery <- summary(delivery_lm) ## check names(summ_delivery)
summ_delivery$sigma ^ 2[1] 10.6summary(delivery_lm)
Call:
lm(formula = time ~ cases + distance, data = delivery_data)
Residuals:
Min 1Q Median 3Q Max
-5.788 -0.663 0.436 1.157 7.420
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 2.34123 1.09673 2.13 0.04417 *
cases 1.61591 0.17073 9.46 3.3e-09 ***
distance 0.01438 0.00361 3.98 0.00063 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 3.26 on 22 degrees of freedom
Multiple R-squared: 0.96, Adjusted R-squared: 0.956
F-statistic: 261 on 2 and 22 DF, p-value: 4.69e-16The second method simply uses the definition of
## method 2
n <- length(delivery_lm$residuals)
(SS_res <- sum(delivery_lm$residuals * delivery_lm$residuals))[1] 234SS_res / (n - 3)[1] 10.6The third method also uses the definition of
## method 3
(SS_res1 <- sum((delivery_data$time - delivery_lm$fitted.values) ^ 2))[1] 234SS_res1 / (n - 3)[1] 10.6Here I show three methods to obtain the
# Method 1: Residual standard error
delivery_ols.mse_resid10.624167155479675The second method simply uses the definition of
# Method 2: Residual Sum of Squares (RSS) and variance estimation
n = len(delivery_ols.resid)
import numpy as np
SS_res = np.sum(delivery_ols.resid ** 2)
SS_res233.73167742055284SS_res / (n - 3)10.624167155479675The third method also uses the definition of
# Method 3: Another way to calculate RSS and variance estimation
SS_res1 = np.sum((delivery_data['time'] - delivery_ols.fittedvalues) ** 2)
SS_res1233.73167742055284SS_res1 / (n - 3)10.62416715547967528.3.3 Wald CI for Coefficients
The
Example: Wald CI for Coefficients
We simply use confint()command with the fitted result put inside to obtain the CI for coefficients.
(ci <- confint(delivery_lm)) 2.5 % 97.5 %
(Intercept) 0.06675 4.6157
cases 1.26182 1.9700
distance 0.00689 0.0219ci = delivery_ols.conf_int()
ci 0 1
Intercept 0.066752 4.615710
cases 1.261825 1.969990
distance 0.006892 0.021878These are marginal CIs separately for each
Covariance of random variables
The covariance matrix of the coefficient vector
The correlation matrix of the coefficient vector
In fact, all
Example: Correlated Coefficients
We use vcov() to obtain the variance-covariance matrix of
## variance-covariance matrix
(V <- vcov(delivery_lm)) (Intercept) cases distance
(Intercept) 1.202817 -0.047263 -8.89e-04
cases -0.047263 0.029150 -5.08e-04
distance -0.000889 -0.000508 1.31e-05(Intercept) cases distance
1.09673 0.17073 0.00361 We can convert the covariance matrix into a correlation matrix using cov2cor(). Clearly
## correlation matrix
cov2cor(V) (Intercept) cases distance
(Intercept) 1.000 -0.252 -0.224
cases -0.252 1.000 -0.824
distance -0.224 -0.824 1.000We use cov_params() to obtain the variance-covariance matrix of
## variance-covariance matrix
V = delivery_ols.cov_params()
V Intercept cases distance
Intercept 1.202817 -0.047263 -0.000889
cases -0.047263 0.029150 -0.000508
distance -0.000889 -0.000508 0.000013## standard error
np.sqrt(np.diag(V))array([1.09673017, 0.17073492, 0.00361309])We can convert the covariance matrix into a correlation matrix using sm.stats.moment_helpers.cov2corr(). Clearly
import statsmodels.api as sm
## correlation matrix
sm.stats.moment_helpers.cov2corr(V)array([[ 1. , -0.25240355, -0.22433649],
[-0.25240355, 1. , -0.824215 ],
[-0.22433649, -0.824215 , 1. ]])How do we specify a confidence level that applies simultaneously to a set of interval estimates? For example, a
The
With repeated sampling, 95% of such ellipses will simultaneously include cases (black point), for example, that are excluded from the marginal interval.
Code
par(mgp = c(2.8, 0.9, 0), mar = c(4, 4, 2, 0))
## confidence region
car::confidenceEllipse(
delivery_lm,
levels = 0.95, fill = TRUE,
which.coef = c("cases", "distance"),
main = expression(
paste("95% Confidence Region for ",
beta[1], " and ", beta[2])
)
)
## marginal CI for cases
abline(v = ci[2, ], lty = 2, lwd = 2)
## marginal CI for distance
abline(h = ci[3, ], lty = 2, lwd = 2)
points(x = 1.4, y = 0.01, col = "red", cex = 2, pch = 16)
points(x = 2, y = 0.008, col = "black", cex = 2, pch = 16)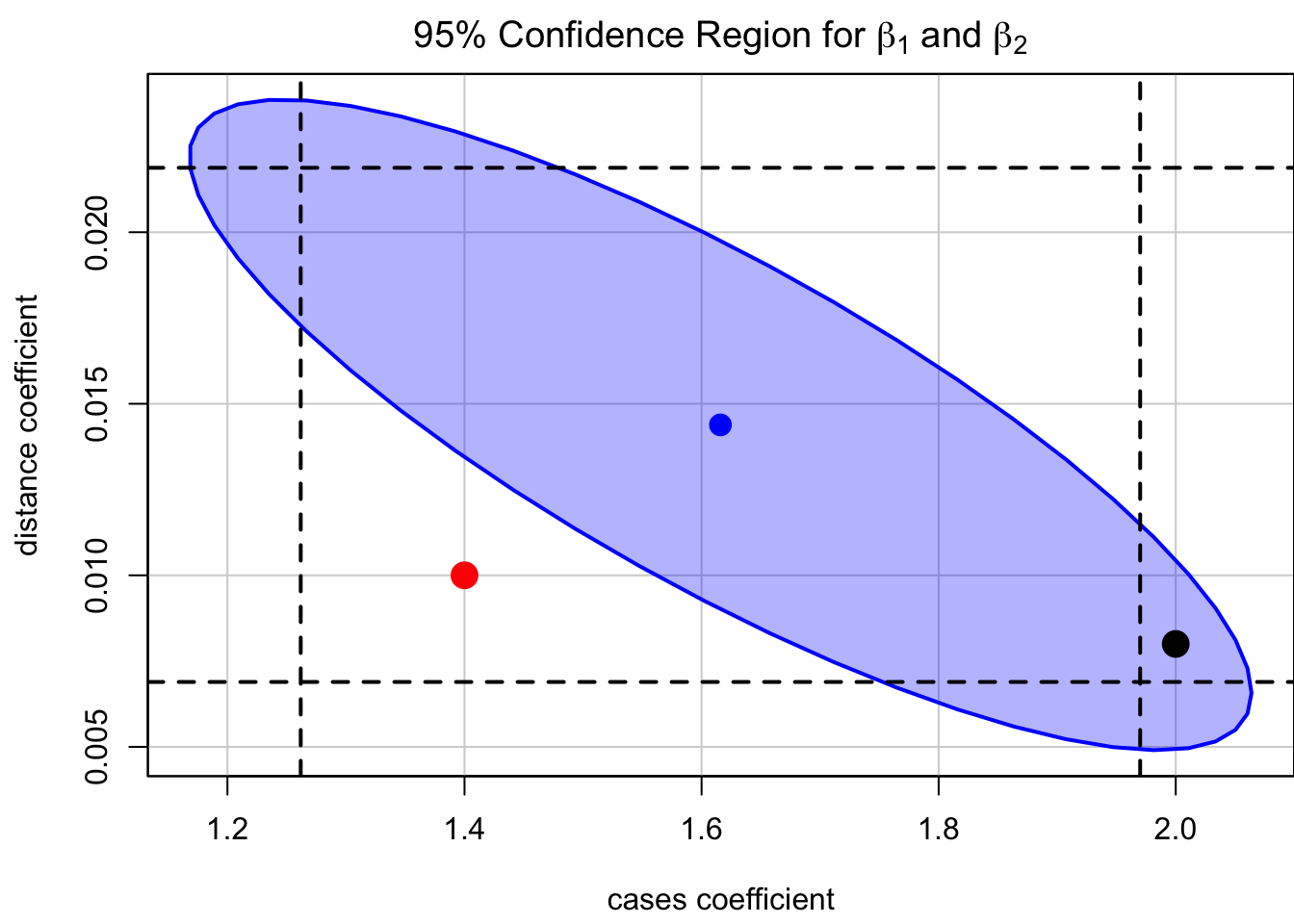
28.3.4 CI for the Mean Response
The fitted value at a point
This is an unbiased estimator for
The
Example: CI for the Mean Response
We learned how to use predict() in the previous chapter. For MLR, we need to specify the 2 predictor values cases = 8, and distance = 275, and save it as a data frame in the newdata argument. Note that the name cases and distance should be exactly the same as their column name of the data delivery_data.
predict(delivery_lm,
newdata = data.frame(cases = 8, distance = 275),
interval = "confidence", level = 0.95) fit lwr upr
1 19.2 17.7 20.8We learned how to use get_prediction() in the previous chapter. For MLR, we need to specify the 2 predictor values cases = 8, and distance = 275, and save it as a DataFrame in the exog argument. Note that the name cases and distance should be exactly the same as their column name of the data delivery_data.
new_data = pd.DataFrame({'cases': [8], 'distance': [275]})
predict = delivery_ols.get_prediction(exog=new_data)
predict.conf_int()array([[17.65389505, 20.79473705]])28.3.5 PI for New Observations
Often we also want to predict the future observation
Example: PI for New Observations
When predicting a new observation with uncertainty, we use interval = "predict". The interpretation is the same as the one in SLR.
predict(delivery_lm,
newdata = data.frame(cases = 8, distance = 275),
interval = "predict", level = 0.95) fit lwr upr
1 19.2 12.3 26.2When predicting a new observation with uncertainty, we use summary_frame(), then grab ‘obs_ci_lower’ and ‘obs_ci_upper’ from the output. The interpretation is the same as the one in SLR.
summary_frame = predict.summary_frame(alpha=0.05)
summary_frame[['obs_ci_lower', 'obs_ci_upper']] obs_ci_lower obs_ci_upper
0 12.284559 26.16407328.3.6 Predictor Effect Plots
A complete picture of the regression surface requires drawing a
Predictor effect plots look at 1 or 2D plots for each predictor.
To plot the predictor effect plot for
fix the values of all other predictors (
substitute these fixed values into the fitted regression equation.
Usually we fix all other predictors (
Example: Predictor Effect Plots
The command predictorEffects() in the effects package is used to generate the predictor effect plots.
library(effects)
plot(effects::predictorEffects(mod = delivery_lm))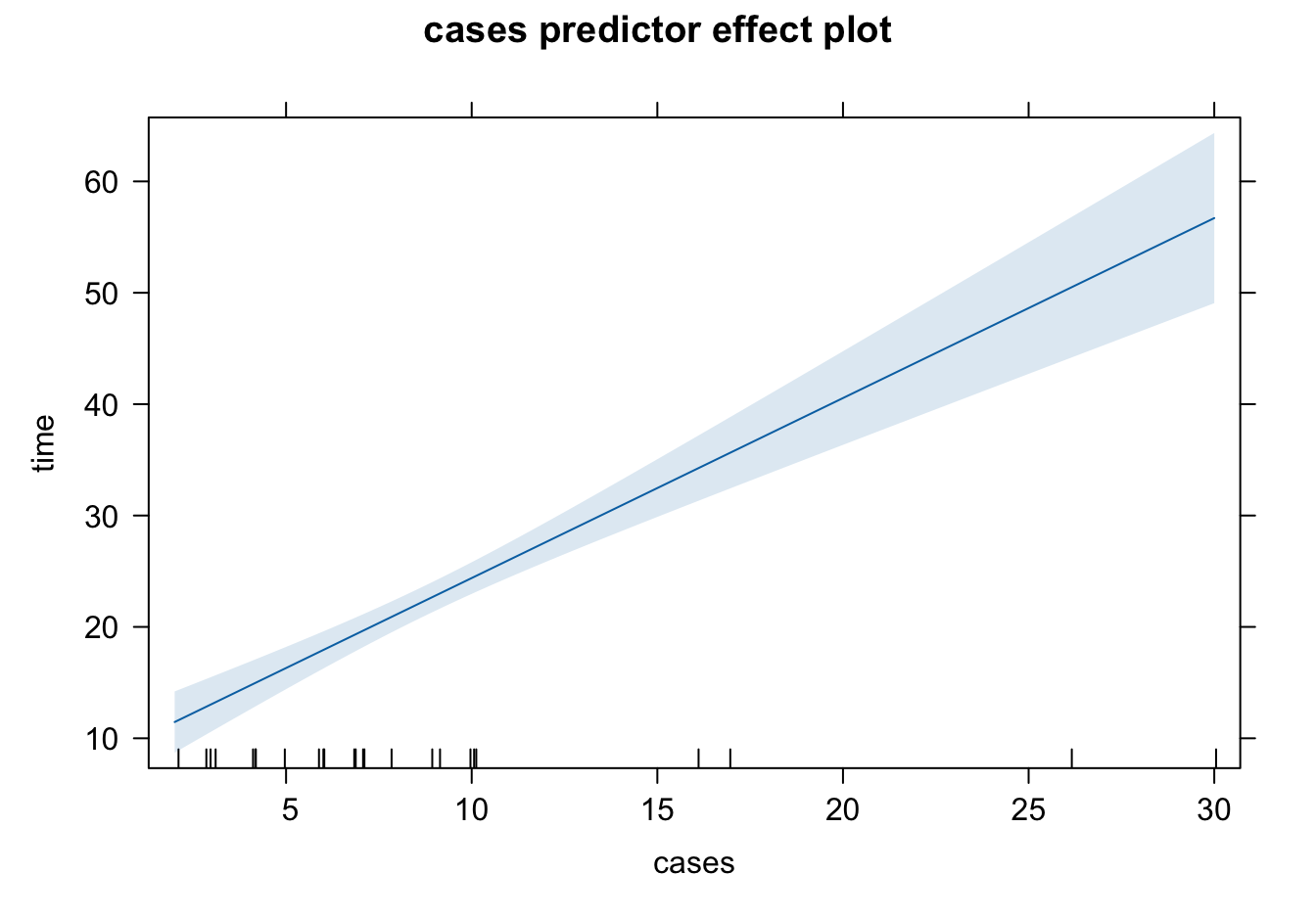
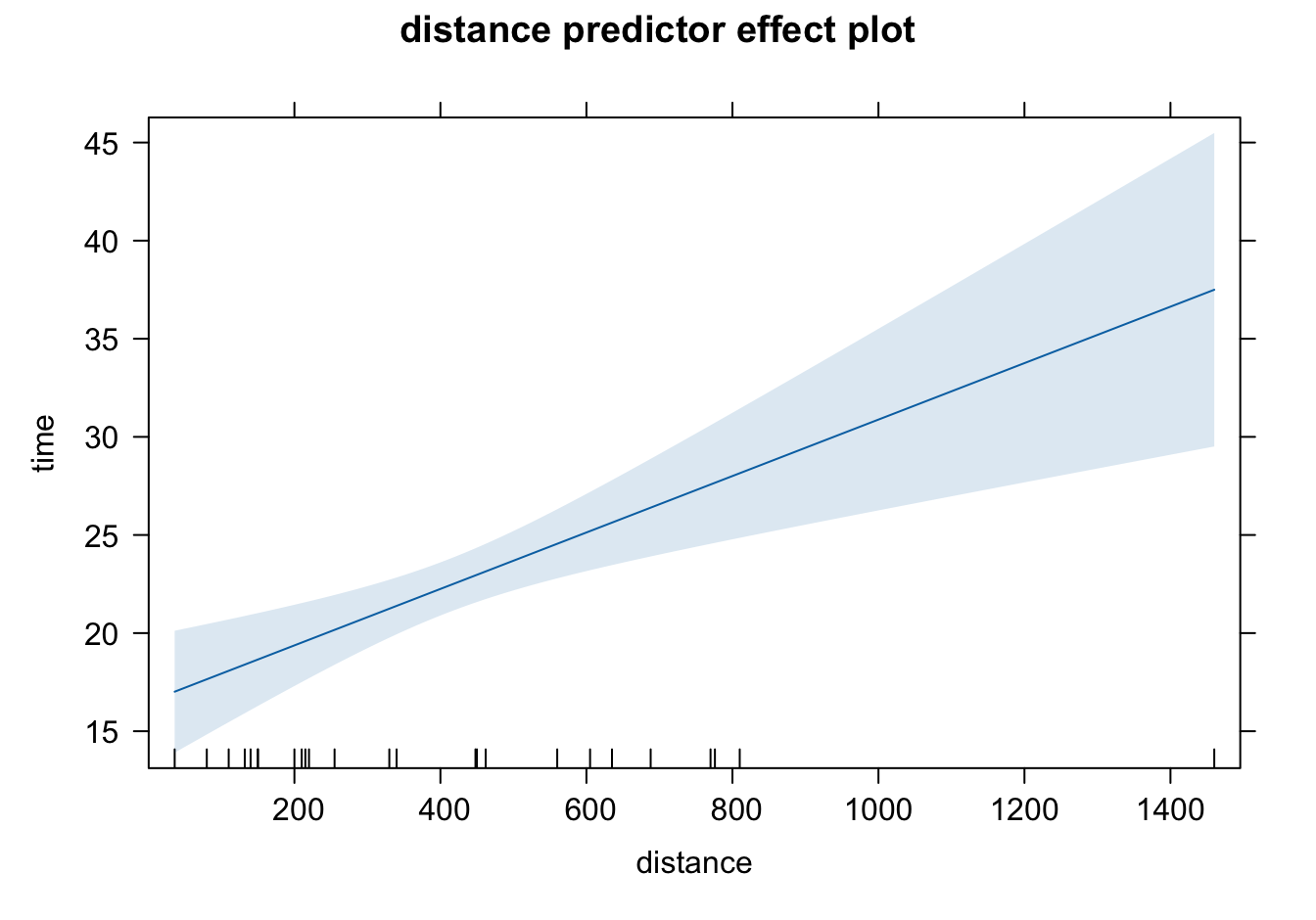
The shaded area represents pointwise 95% confidence interval about the fitted line, without correction for simultaneous statistical inference. The short vertical lines at the bottom indicate the values of predictors. The interval length is larger when the predictor value is away from its average. Since our model is linear, the mean of time increases linearly as cases or distance increases.
So far to my knowledge there is no Python function for creating predictor effect plots. However, statsmodels does offer other useful regression plots.
28.4 Hypothesis Testing
In this section we talk about two tests: Test for significance of regression and Tests on individual coefficients. In fact, one can test whether or not the coefficients form any linear combination relationship, called the general linear hypotheses. We leave this part of discussion in the Regression Analysis course.
28.4.1 Test for Significance of Regression
Test for significance determines if there is a linear relationship between the response and any of the regressor variables. In other words, we are testing
As long as there is one predictor has a significant impact on the response,
The test is usually conducted by checking the ANOVA table of MLR as shown below. When
| Source of Variation | SS | df | MS | F |
|
|---|---|---|---|---|---|
| Regression | |||||
| Residual | |||||
| Total |
We reject
We may reject the null when the truth is all beta’s are nonzero, or only one single beta is nonzero. And we may need further post hoc analysis to see which coefficients are nonzero.
If there is only one nonzero coefficient, and we reject the null, basically, the nearly all the variation of
Example: Test for Significance
If we check the summary of the fitted result, it shows some t values and p-values, but no ANOVA table shows up.
summ_delivery...
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 2.34123 1.09673 2.13 0.04417 *
cases 1.61591 0.17073 9.46 3.3e-09 ***
distance 0.01438 0.00361 3.98 0.00063 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 3.26 on 22 degrees of freedom
Multiple R-squared: 0.96, Adjusted R-squared: 0.956
F-statistic: 261 on 2 and 22 DF, p-value: 4.69e-16
...If we check the summary of the fitted result, it shows some t values and p-values, but no ANOVA table shows up.
delivery_ols.summary()| Dep. Variable: | time | R-squared: | 0.960 |
| Model: | OLS | Adj. R-squared: | 0.956 |
| Method: | Least Squares | F-statistic: | 261.2 |
| Date: | Tue, 15 Oct 2024 | Prob (F-statistic): | 4.69e-16 |
| Time: | 10:36:45 | Log-Likelihood: | -63.415 |
| No. Observations: | 25 | AIC: | 132.8 |
| Df Residuals: | 22 | BIC: | 136.5 |
| Df Model: | 2 | ||
| Covariance Type: | nonrobust |
| coef | std err | t | P>|t| | [0.025 | 0.975] | |
| Intercept | 2.3412 | 1.097 | 2.135 | 0.044 | 0.067 | 4.616 |
| cases | 1.6159 | 0.171 | 9.464 | 0.000 | 1.262 | 1.970 |
| distance | 0.0144 | 0.004 | 3.981 | 0.001 | 0.007 | 0.022 |
| Omnibus: | 0.421 | Durbin-Watson: | 1.170 |
| Prob(Omnibus): | 0.810 | Jarque-Bera (JB): | 0.010 |
| Skew: | 0.032 | Prob(JB): | 0.995 |
| Kurtosis: | 3.073 | Cond. No. | 873. |
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
How do we obtain the ANOVA Table?
| Source of Variation | SS | df | MS | F |
|
|---|---|---|---|---|---|
| Regression | |||||
| Residual | |||||
| Total |
We may think using anova(delivery_lm) as we do for SLR.
anova(delivery_lm) ## This is for sequential F-testAnalysis of Variance Table
Response: time
Df Sum Sq Mean Sq F value Pr(>F)
cases 1 5382 5382 506.6 < 2e-16 ***
distance 1 168 168 15.8 0.00063 ***
Residuals 22 234 11
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1We may think using sm.stats.anova_lm(delivery_ols) as we do for SLR.
sm.stats.anova_lm(delivery_ols) df sum_sq mean_sq F PR(>F)
cases 1.0 5382.408797 5382.408797 506.619363 1.112549e-16
distance 1.0 168.402126 168.402126 15.850854 6.312469e-04
Residual 22.0 233.731677 10.624167 NaN NaNUnfortunately, this ANOVA table is so called Type-I ANOVA table in literature for a sequential F-test, which is NOT what we want.
To obtain the correct ANOVA table, we need to view the test in a different way. Testing coefficients is like model comparison: We are comparing two models, the full model having all the predictors
Full model:
Null model:
The idea is that we are trying to see how close the full model fitting is close to the null model fitting. If
In our example,
Full model: including both
casesanddistancepredictorsNull model: no predictors
The ANOVA table for the example is

To generate the ANOVA table using R, we first create the null model and save its fitted result. When there is no predictors in the model, we write time ~ 1 where 1 represents the intercept term. Then we are comparing the two model fitted results using anova(null_lm, delivery_lm).
## regression with intercept only
null_lm <- lm(time ~ 1, data = delivery_data)
anova(null_lm, delivery_lm)...
Analysis of Variance Table
Model 1: time ~ 1
Model 2: time ~ cases + distance
Res.Df RSS Df Sum of Sq F Pr(>F)
1 24 5785
2 22 234 2 5551 261 4.7e-16 ***
...Notice that the output is not exactly the same as the ANOVA table, but both are equivalent. We just need to carefully and correctly interpret the R output. The first row shows the RSS column. RSS is the residual sum of squares
The second row provides information about Sum of Sq, and RSS.
In Row 2, Res.Df is the residual degrees of freedom, and Df is the regression degrees of freedom. The value 24 in Row 1, the residual degrees of freedom of the null model, is worked as the total degrees of freedom, the same idea that its
To generate the ANOVA table using Python, we first create the null model and save its fitted result. When there is no predictors in the model, we write time ~ 1 where 1 represents the intercept term. Then we are comparing the two model fitted results using sm.stats.anova_lm(null_ols, delivery_ols).
## regression with intercept only
null_ols = ols('time ~ 1', data=delivery_data).fit()
sm.stats.anova_lm(null_ols, delivery_ols) df_resid ssr df_diff ss_diff F Pr(>F)
0 24.0 5784.542600 0.0 NaN NaN NaN
1 22.0 233.731677 2.0 5550.810923 261.235109 4.687422e-16Notice that the output is not exactly the same as the ANOVA table, but both are equivalent. We just need to carefully and correctly interpret the Python output. The first row shows the ssr column. ssr is the sum of squares residual
The second row provides information about ss_diff, and ssr.
In Row 2, df_resid is the residual degrees of freedom, and df_diff is the regression degrees of freedom. The value 24 in Row 1, the residual degrees of freedom of the null model, is worked as the total degrees of freedom, the same idea that its
The output does not provide the mean square information, but it can be easily calculated.
28.4.2
We learn in SLR that
The model with one additional predictor always gets a higher
While this approach might yield a model that fits the current data very well, it poses significant risks if our goal is to predict new, unseen future data. Including too many variables in the regression model can lead to overfitting—a situation where the model fits the sample data exceptionally well but performs poorly when predicting the mean response or new response values for a different dataset. Overfitting results in a model that captures noise and idiosyncrasies of the sample data, rather than the underlying patterns, making it less generalizable and less reliable for future predictions.
A complex or a larger model has several other disadvantages. First, it’s more difficult to interpret your model and results. It reduces the interpretability. Second, the computing or running time is usually longer, and sometimes much longer depending on the order of complexity. Also, the data or the model itself may consume lots of memory spaces.
Occam’s Razor: Don’t use a complex model if a simpler model can perform equally well!
There are other criterion or metrics for accessing model adequacy or model fit that may be better than
For a model with 3 predictors,
The 4-th regressor is added into the model, and
The new added regressor should have explanatory power for
Example:
To get
summ_delivery...
Residual standard error: 3.26 on 22 degrees of freedom
Multiple R-squared: 0.96, Adjusted R-squared: 0.956
...summ_delivery$r.squared[1] 0.96summ_delivery$adj.r.squared[1] 0.956To get
delivery_ols.summary()| Dep. Variable: | time | R-squared: | 0.960 |
| Model: | OLS | Adj. R-squared: | 0.956 |
| Method: | Least Squares | F-statistic: | 261.2 |
| Date: | Tue, 15 Oct 2024 | Prob (F-statistic): | 4.69e-16 |
| Time: | 10:36:46 | Log-Likelihood: | -63.415 |
| No. Observations: | 25 | AIC: | 132.8 |
| Df Residuals: | 22 | BIC: | 136.5 |
| Df Model: | 2 | ||
| Covariance Type: | nonrobust |
| coef | std err | t | P>|t| | [0.025 | 0.975] | |
| Intercept | 2.3412 | 1.097 | 2.135 | 0.044 | 0.067 | 4.616 |
| cases | 1.6159 | 0.171 | 9.464 | 0.000 | 1.262 | 1.970 |
| distance | 0.0144 | 0.004 | 3.981 | 0.001 | 0.007 | 0.022 |
| Omnibus: | 0.421 | Durbin-Watson: | 1.170 |
| Prob(Omnibus): | 0.810 | Jarque-Bera (JB): | 0.010 |
| Skew: | 0.032 | Prob(JB): | 0.995 |
| Kurtosis: | 3.073 | Cond. No. | 873. |
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
delivery_ols.rsquared0.9595937494832257delivery_ols.rsquared_adj0.955920453981700828.4.3 Tests on Individual Regression Coefficients
This is the hypothesis test on any single regression coefficient:
It is a
We can also do a one-side test for sure. But I am not sure if there is a R function to do a one-sided test. But we can always compute the test statistic or the p-value ourselves.
Example: Tests on Individual Coefficients
Suppose we would like to assess the effect of
The marginal test results are shown in the summary of fitted result. The t test statistic value is 3.98, and p-value is close to zero, concluding that
summ_delivery$coefficients Estimate Std. Error t value Pr(>|t|)
(Intercept) 2.3412 1.09673 2.13 4.42e-02
cases 1.6159 0.17073 9.46 3.25e-09
distance 0.0144 0.00361 3.98 6.31e-04The marginal test results are shown in the summary of fitted result. The t test statistic value is 3.98, and p-value is close to zero, concluding that
delivery_ols.summary()| Dep. Variable: | time | R-squared: | 0.960 |
| Model: | OLS | Adj. R-squared: | 0.956 |
| Method: | Least Squares | F-statistic: | 261.2 |
| Date: | Tue, 15 Oct 2024 | Prob (F-statistic): | 4.69e-16 |
| Time: | 10:36:46 | Log-Likelihood: | -63.415 |
| No. Observations: | 25 | AIC: | 132.8 |
| Df Residuals: | 22 | BIC: | 136.5 |
| Df Model: | 2 | ||
| Covariance Type: | nonrobust |
| coef | std err | t | P>|t| | [0.025 | 0.975] | |
| Intercept | 2.3412 | 1.097 | 2.135 | 0.044 | 0.067 | 4.616 |
| cases | 1.6159 | 0.171 | 9.464 | 0.000 | 1.262 | 1.970 |
| distance | 0.0144 | 0.004 | 3.981 | 0.001 | 0.007 | 0.022 |
| Omnibus: | 0.421 | Durbin-Watson: | 1.170 |
| Prob(Omnibus): | 0.810 | Jarque-Bera (JB): | 0.010 |
| Skew: | 0.032 | Prob(JB): | 0.995 |
| Kurtosis: | 3.073 | Cond. No. | 873. |
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
Each piece of information can be obtained from the fiited object.
delivery_ols.paramsIntercept 2.341231
cases 1.615907
distance 0.014385
dtype: float64delivery_ols.bseIntercept 1.096730
cases 0.170735
distance 0.003613
dtype: float64delivery_ols.tvaluesIntercept 2.134738
cases 9.464421
distance 3.981313
dtype: float64delivery_ols.pvaluesIntercept 4.417012e-02
cases 3.254932e-09
distance 6.312469e-04
dtype: float6428.5 Inference Pitfalls
- The test
- Consider the practical significance of the result, not just the statistical significance.
- Use the confidence interval to draw conclusions instead of relying only p-values.
- If the sample size is small, there may not be enough evidence to reject
- DON’T immediately conclude that the variable has no association with the response.
- There may be a linear association that is just not strong enough to detect given your data, or there may be a non-linear association.
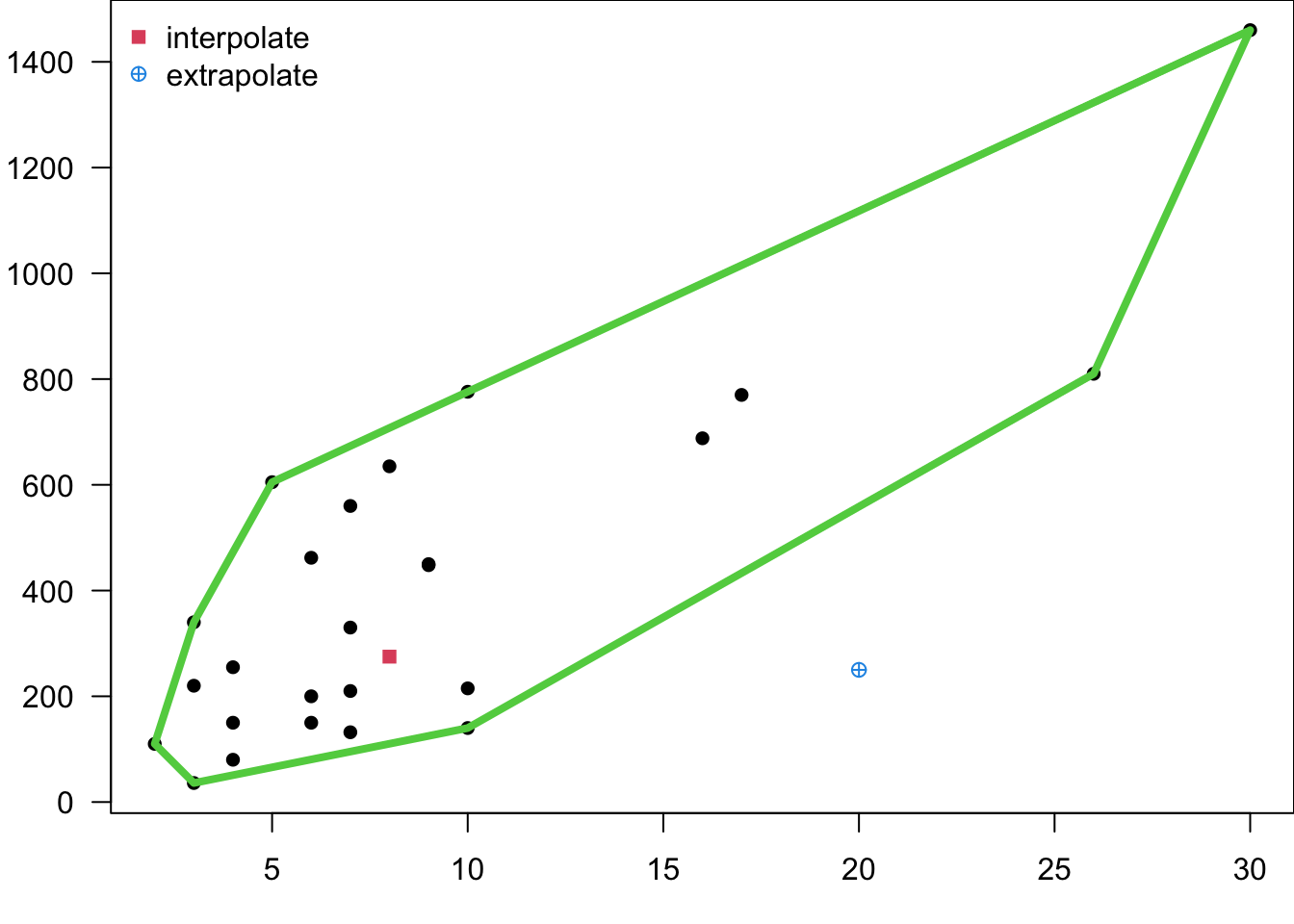
- In MLR, it’s easy to inadvertently extrapolate since the regressors jointly define the region containing the data. We can define the smallest convex set containing all of the original